Однородные СЛАУОднородной системой линейных уравнений называется система вида:
Нулевое решение Однородные системы всегда совместны, т.к. всегда существует тривиальное решение. Если существует любое ненулевое решение системы, то оно называется нетривиальным. Решения однородной системы обладают свойством линейности: Решим систему Перепишем её в матричном виде:
Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:
Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует Перепишем полученную систему в виде уравнений:
Возьмём
Подставим по очереди единицы в качестве одной из свободных переменных:
Тогда общее решение рассматриваемой системы может быть записано так:
а вектора
|
системы (1) называется тривиальным решением.
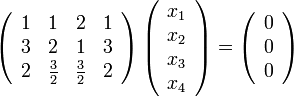
линейно независимых решения системы.
и 
в качестве главных переменных. Тогда:
и 
.
,
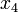составляют фундаментальную систему решений.
