Матрицы, имеющие одинаковый ранг, называются эквивалентными. Под элементарными преобразованиями над матрицами понимают:
- Умножение строки (столбца) матрицы на число, отличное от нуля.
- Прибавление к одной строке (столбцу) матрицы другой строки (столбца), умноженной на число.
- Перемена местами двух строк (столбцов) матрицы.
При элементарных преобразованиях ранг матрицы не изменятся. При вычислении ранга матрицы целесообразно провести такие элементарные преобразование, которые привели бы к эквивалентной матрице, ранг которой найти несложно. В частности такими матрицами являются диагональные или трапециевидные матрицы, например: 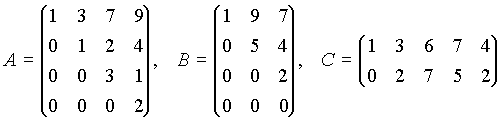 .
.
rang(A) = 4, rang(B) =3, rang(C) =2.
Справедливы следующие утверждения:
- Если каждый элемент матрицы равен нулю, то ранг матрицы равен нулю.
- Если к матрице приписать строчку (столбец), состоящую из нулей, то ранг матрицы не изменится.
- Если в матрице все миноры k -го порядка равны нулю, то равны нулю и все миноры более высокого порядка (если таковые существуют).

 .
.


