Определители 2-го и 3-го порядка и их свойства
Понятие определителя - число, характеризующее квадратную матрицу Определитель матрицы 1) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
Пример. Вычислить определитель матрицы 3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
Данная формула получила название правила треугольников или правило Сарруса. При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:
Свойства определителей 1. Если какая-либо строка (столбца) матрицы состоит из одних нулей, то ее определитель равен 0. 2. Если все элементы какой-либо строки (столбца) матрицы умножить на число Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов. 3. При транспонировании матрицы ее определитель не изменяется: 4. При перестановки двух строк (столбцов) матрицы ее определитель меняет знак на противоположный. 5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0. 6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0. 7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0. 8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число. 9. Сумма произведений произвольных чисел 10. Определитель произведения двух квадратных матриц равен произведению их определителей:
|

 , необходимо для решения систем линейных алгебраических уравнений.
, необходимо для решения систем линейных алгебраических уравнений.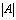 ,
,  ,
,  .
. . Произведения
. Произведения  называются членами определителя 2-го порядка.
называются членами определителя 2-го порядка.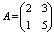 . Р е ш е н и е.
. Р е ш е н и е. 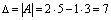 .
.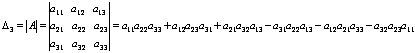
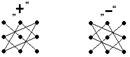
 ,то ее определитель умножится на это число
,то ее определитель умножится на это число  .
. на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа
на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа 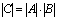 , где
, где 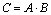 , а
, а  - матрицы
- матрицы  -го порядка.
-го порядка.


