Теоретические основы вычисления оценок эффективности отбора
Тема: Оценка эффективности отбора.
Вопросы 1. Теоретические основы вычисления оценок эффективности отбора. 2. Расчет величины селекционного дифференциала. 3. Факторы, влияющие на эффективность обора.
Ключевые слова: отбор, эффект селекции, селекционный дифференциал, интенсивность отбора, измерение и прогноз действия отбора, повышение селекционного дифференциала.
Литература
1. Гужов Ю.Л., Фукс А., Валичек П. Селекция и семеноводство культурных растений. – М.: Агропромиздат,1991. – 463 с. – (Учебники и учеб. Пособия для студентов высш. Учеб. Заведений). 2. Рокицкий. 3. Бессчетнов В.П. Полиморфизм казахстанских популяций облепихи крушиновидной (Hippophae rhamnoides L.) по хозяйственным и адаптивным признакам. Дис. док. биол. наук. Алматы, 1994. – 543 с. 4. Бессчетнов В.П. 5. Чмыр А.Ф., Бессчетнов В.П. Экология и культура облепихи Hippophae rhamnoides L. – СПб, СПбНИИЛХ, 1998. – 278 с. 6. Котов М.М. Генетика и селекция. Часть 1.: Учебник для вузов. – Йошкар-Ола: МарГТУ, 1997. – 280 с. 7. Котов М.М. Генетика и селекция. Часть 2.: Учебник для вузов. – Йошкар-Ола: МарГТУ, 1997. – 108 с. 8. Любавская А.Я. Лесная селекция и генетика.: Учебник для вузов. – М.: Лесная промышленность, 1982. – 288 с. 9. Джонатан В. Райт. Введение в лесную генетику. М.: Лесная промышленность, 1978. – 470 с.
Теоретические основы вычисления оценок эффективности отбора
Оценка эффективности отбора представляет собой одну из важных (серьезных) задач селекции, в частности селекции методом отбора (а в широком смысле – селекции как формы деятельности человека в целом). Для её реализации используют специальные оценочные критерии, называемые селекционным дифференциалом и интенсивностью отбора. Проведение отбора по фенотипу, в частности отбор плюсовых деревьев (потомство которых используется для создания ЛСП-1) будет эффективным при высоком уровне аддитивной (не связана с эффектом доминирования, а определяемой собственно набором генов) наследственности, а также будет зависеть от проявления эффекта доминирования (полного или неполного, а также кодоминирования и эффектом межаллельного взаимодействия в целом). В общем, этот фактор рассматривают как генотипический.
Аддитивная наследственность в селекции рассматривается как наследственность, обусловленная собственно набором генов, без учета эффекта их аллельного (доминирование) взаимодействия. Такая наследственность часто называется истинной и оценивается коэффициентом наследуемости в узком смысле. Аддитивная наследственность – это наследственность, обусловленная суммирующим эффектом полимерно действующих генов (расширить и уточнить определение понятия аддитивная наследственность и понятия неаддитивная наследственность; возможно эпистаз, плейотропия, полимерная наследственность, комплементарность, гены модификаторы).
Кроме того, эффективность отбора будет определяться тем, насколько велико влияние факторов среды на формирование фенотипических признаков, т.е. будет зависеть от так называемой средовой компоненты вариансы или остаточной дисперсии признака. Влияние среды выражается в возникновении (приобретении) у представителей популяции разнообразных ненаследуемых изменений (уклонений от среднего) значения признака. В целом они (флуктуации) расширяют фенотипическое разнообразие исходного материала. Однако целью и желаемым результатом любого отбора в селекции всегда является отбор лучших генотипов, а не фенотипов (о чем мы уже говорили, рассматривая проблемы, стоящие перед современной селекцией). Модифицирующее влияние среды в такой ситуации будет усложнять работу по отбору лучших генотипов. Чем сильнее выражено такое модифицирующее влияние среды, тем сложнее организовать эффективный отбор лучших генотипов, тем больше шансов при отборе по фенотипу, что имеет место в лесной селекции, «отобрать» не собственно «лучший» генотип, а лишь видимую нами ненаследуемую часть фенотипических проявлений признака, которая не сохранится при семенном размножении или в иных условиях. Это в конечном итоге снизит результаты или эффективность отбора, если под отбором понимать именно отбор лучших генотипов. Результативность (окончательная результативность) отбора определяется и заданным уровнем отбора (заданной «жесткостью» или «строгостью» или «интенсивность» отбора), который в свою очередь определяется задачами селекции и принятым в каждом конкретном случае порядком проведения селекционных мероприятий. В конечном итоге определяется селекционером.
пример. В лесной селекции селекционный дифференциал при заданном уровне интенсивности отбора – «заданный селекционный дифференциал» – используется при выделении плюсовых деревьев или плюсовых насаждений. «Правилами» (дать расширенную трактовку «Правил» и заложенных в них нормативов) устанавливается величина селекционного дифференциала, заданного в процентах (%), который должен быть достигнут при отборе плюсового дерева. Так по высоте плюсовое дерево должно превосходить среднее популяционное (в насаждении) на 10 %, а по диаметру – на 30 %. Ранее существовали еще более жесткие требования к отбираемым плюсовым деревьям: по высоте 20 – 25%, по диаметру 30 – 35%. Эти заданные превышения значений установленных признаков (высоты и диаметра) и представляют собой селекционный дифференциал при отборе плюсовых деревьев.
Уровень интенсивности отбора зависит от того, сколько наилучших особей будет отобрано из популяции (из исходной совокупности в общем случае), например: 15 самых лучших или 10 самых лучших, или только 5 самых лучших, или в конечном итоге только одно (1) самое лучшее дерево; или тем, какой предел проявления признака признается достаточным для включения особи в число отобранных: все особи с высотой 32 м и более, или все особи с высотой 33 м и более, или, наконец, все особи с высотой 35 м и более и т.п.
Для популяций древесных и кустарниковых пород характерно промежуточное наследование, что связано аддитивной наследственностью большинства количественных признаков и определено эволюционным процессом. Аддитивный характер наследования основных количественных признаков деревьев и кустарников приводит к возникновению множества постепенно переходящих друг в друга количественных его проявлений (чем больше полимерно действующих генов, тем сильнее проявление признака).
При отборе по фенотипу (отбор плюсовых деревьев и насаждений) результат будет определяться рядом условий: - тем, насколько велика доля наследственной обусловленности проявлений признака или, что то же самое, генотипической обусловленности изменчивости признака, в общей, учитываемой нами при отборе фенотипической изменчивости признака у селектируемых особей, от степени генетической детерминированности признака, от степени его стабильности; - тем, какова доля средовой дисперсии признака или доля влияния факторов среды на его проявление, от его лабильности, от подверженности признака влиянию факторов среды; - в конечном итоге фенотипическое проявление признака, то на что направлен отбор по фенотипу, будет зависеть от соотношения долей влияния на проявление фенотипа факторов наследственности (генотипа или идиотипа в широком смысле) и факторов среды (доля ненаследственной изменчивости).
Это позволяет рассматривать взаимное действие (оно всегда именно таково) факторов среды и факторов наследственности на формирование фенотипа особи как действие одного фактора – фактора соотношения между долями влияния среды и генотипа.
Тогда эффект отбора по количественным признакам можно представить как результат, (определяемый) зависящий от действия двух формально независимых друг от друга комплексных факторов (доля влияния фактора среды, формально зависит от величины генотипической вариансы): - от интенсивности отбора, определяемой задачами селекции и планом селекционных мероприятий; - от силы модифицирующего влияния среды, под которой понимают долю ненаследственной изменчивости в общей фенотипической изменчивости, рассматривая её как оценку соотношения «наследственность/среда».
Для планирования и прогнозирования процесса отбора важно дать оценку влияния этих двух факторов.
Эффективность или результативность отбора можно оценить двумя широко применяемыми показателями: - показателем селекционного дифференциала (обозначим его S); - показателем интенсивности отбора (обозначим его i).
В большинстве отечественных публикаций эти два показателя оценок эффективности отбора рассматриваются как самостоятельные величины, а в ряде публикаций зарубежных авторов (Райт, 1975) – как одна величина.
Относительную силу (долю) воздействия генетического влияния и влияния внешней среды на фенотипическое проявление признака оценивают (измеряют) с помощью коэффициента наследуемости (H2), который выражается в долях от единицы или в процентах (%%). Например, Н2 = 0,78 или 78%. Это значит, что проявление признака на 78% обусловлено генотипически, а на 22% – условиями среды.
Селекционный дифференциал – это разность между средней величиной признака в совокупности отобранных особей и соответствующей средней величиной того же признака в исходной популяции.
Селекционный дифференциал – это разность между средней и отобранными деревьями, семьями или клонами (Райт, 1978, стр. 160).
Дж. В. Райт (1978, стр. 160 – 162) рассматривает селекционный дифференциал как один из показателей эффективности отбора, в том числе отбора по фенотипу плюсовых деревьев, отбора, проводимого по результатам испытания потомств – семей, или клонов.
ПРИМЕР: Если средняя высота деревьев в насаждении (популяции) составляет 30 метров, а средняя высота группы отобранных деревьев составляет 33 метра, то селекционный дифференциал составит 33 – 30 = 3 м, или 10% (от исходной популяционной величины). Если при испытании семенного потомства (испытательные культуры в Семеновском спецсемлесхозе в Осинках) средняя высота всего потомства в испытательных культурах 20 м, а высота отобранного потомства от одного плюсового дерева – 21 м, то селекционный дифференциал равен 21 – 20 = 1 м, или 5% (по Райту, 1978, стр. 161).
В лесном хозяйстве отобранными растениями являются плюсовые деревья, выделенные по комплексу положительных фенотипических признаков, имеющих хозяйственное и адаптационное значение, их семенное потомство (полусибсовые семьи), клоновые репродукции (прививочные плантации и архивы клонов).
Выражают селекционный дифференциал в натуральных единицах измерения значений признака, например: высота – в м; диаметр ствола на высоте 1.3 метра – в см; объем ствола – в м3; площадь поперечного сечения ствола – в см2 и т.д. При этом могут также использоваться как относительные размерные показатели (отношение высоты ствола, выраженной в метрах к площади поперечного сечения ствола, выраженной в см2 – м/см2; плотность древесины – г/см3 и т.д.), так и безразмерные величины (отношение длины листовой пластинки, выраженной в см, к ширине листовой пластинки, выраженной в сантиметрах, называется коэффициентом формы и выражается безразмерной величиной; аналогично выражается коэффициент формы шишек или семян и т.п.). Эта форма выражения селекционного дифференциала наиболее предметна, наглядна и легко воспринимается. Она позволяет оценить эффективность отбора, проводимого на разных объектах, но по одному и тому же показателю, например, по высоте ствола и его объему. Вместе с тем понятно, что такая форма выражения селекционного дифференциала не позволяет сопоставлять эффективность отбора, проводимого по разным признакам: высоте ствола (в метрах) и диаметру ствола (в сантиметрах), даже если отбор ведется в одной и той же популяции.
В этой связи для получения сопоставимой оценки эффективности отбора, проводимого по разным признакам, селекционный дифференциал выражают в процентах от среднего значения признака в исходной совокупности – в популяции, из которой проведен отбор. Понятно, что при такой оценке в относительных величинах (процент от числа есть величина относительная или доля) дать сравнительную оценку эффективности отбора любых самых разных признаков, и указать, по какому признаку отбор оказался более эффективным, а по какому – менее эффективным, достаточно просто.
Селекционный дифференциал, выраженный в натуральных величинах, как мера интенсивности отбора имеет серьезный недостаток: по величине селекционного дифференциала интенсивность (строгость) отбора по определенному признаку в различных популяциях можно сравнить только в том случае, если изучаемые популяции имеют одинаковую изменчивость определенного признака. В природе это условие обычно не обнаруживается, и популяции, как правило, характеризуются различными уровнями изменчивости по анализируемым признакам. Это справедливо в отношении практически всех хозяйственно важных и адаптивных признаков у большинства лесных деревьев и кустарников. Понятно, что по признаку с большей дисперсией, будет достигнут и заведомо больший результат, и, наоборот – для признака с меньшей дисперсией результат окажется меньшим. Тогда сравнение эффективности отбора по признакам, имеющим разную дисперсию, будет не вполне корректным, даже если её оценку выразить в процентах.
Однако, хорошо известно то, что оценка эффективности отбора зависит от дисперсии признака.
Для преодоления этого обстоятельства при получении сопоставимых оценок эффективности отбора, независимых от уровня изменчивости признака, применяют показатель, выражающий селекционный дифференциал в долях от среднего квадратического отклонения данного признака в исходной популяции (мы обозначили его как sр). Этот показатель получил название «интенсивность отбора». Он представляет собой отношение величины селекционного дифференциала, выраженного в натуральных единицах измерения, к величине дисперсии признака в исходной популяции, из которой был произведен отбор, выраженной в тех же единицах. Легко заметить, что показатель интенсивности отбора есть величина относительная и безразмерная, поскольку в получаемом отношении участвуют только одноразмерные величины.
Интенсивность отбора – это показатель, определяющий, какую долю от среднего кадратического отклонения признака в исходной популяции составляет достигнутый при отборе селекционный дифференциал.
Интенсивность отбора является относительным (удельным) показателем, не зависящим от уровня изменчивости (дисперсии) признака в разных популяциях, и позволяет сравнивать уровень интенсивности отбора в любом числе популяций при специфике характера изменчивости признака в каждой из них. Интенсивность отбора показывает, какое число «сигм» содержит селекционный дифференциал.
Формула его расчета достаточна проста:
i – интенсивность отбора; S – селекционный дифференциал; σp – среднее квадратическое отклонение признака в популяции.
|

 ,
,  где
где - селекционный дифференциал;
- селекционный дифференциал; - среднее значение признака в отобранной группе растений (от extraction – выделение, экстракция) или одним растением, которые могут быть отобранными по фенотипу плюсовыми деревьями, отобранными лучшими семьями при испытании семенных потомств, отобранными лучшими вегетаивными потомствами в клоновом отборе;
- среднее значение признака в отобранной группе растений (от extraction – выделение, экстракция) или одним растением, которые могут быть отобранными по фенотипу плюсовыми деревьями, отобранными лучшими семьями при испытании семенных потомств, отобранными лучшими вегетаивными потомствами в клоновом отборе;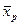 - среднее значение признака в популяции, из которой отобрана группа особей (от population – популяция), рассматривается как собственно природная популяция, так и как исходная группа особоей, из числа которой производят отбор.
- среднее значение признака в популяции, из которой отобрана группа особей (от population – популяция), рассматривается как собственно природная популяция, так и как исходная группа особоей, из числа которой производят отбор. , где
, где


