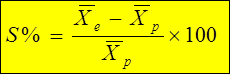Расчет величины селекционного дифференциала.
Рассмотри алгоритм расчета величины селекционного дифференциала на одном из примеров.
ЗАДАНИЕ 1. Рассчитайте величину оценок эффективности отбора: селекционного дифференциала и интенсивности отбора, - по предложенным заданиям (задания прилагаются в форме дидактического материала).
Задача 1. Рассчитайте величину достигнутого при отборе селекционного дифференциала по предложенным вариантам дидактического материала (дидактический материал определяется преподавателем).
ПОРЯДОК ВЫПОЛНЕНИЯ РАСЧЕТОВ
1. Поскольку получение оценок селекционного дифференциала предусматривает сравнение двух средних величин (сравнение средних величин двух статистических совокупностей), рассчитывают средние значения одного из селектируемых признаков в группе отобранных особей (совокупности плюсовых растений), и для популяции в целом (исходного насаждения). Применяем общепринятый алгоритм расчетов с определением следующих основных статистик для каждой из совокупностей: и для исходной популяции, и для группы отобранных лучших особей.
Где:
Vi – даты или варианты наблюдений, отдельные измерения – частные значения признака. e - индекс отобранной группы (от слова extraction – экстракция, выделили, отобрали). p – индекс популяции (от слова population – популяция). ∑ - знак суммы. i – порядковый номер варианта, i= от 1 до n. n - численность статистической совокупности. Для популяции n = численности популяции, для отобранной группы отселектирванных особей n равно числу отобранных особей. В ситуации, когда параметры популяции оцениваю по результатам анализа выборки, численность популяции – это численность особей на пробной площади, то есть численность выборки. σ – среднее квадратическое отклонение (в Excel – это стандартное отклонение), показывает, на сколько в среднем в ту или иную сторону от среднего статистического значения признака отклоняется каждое отдельное частное значение признака в выборке, которое может быть больше или меньше среднего (что показывает знак ±). m – ошибка репрезентативности выборочного среднего, показывает на какую величину в большую или меньшую сторону от генерального среднего может отличаться вычисленное среднее для конкретной выборки. Cv – коэффициент вариации, показывает какую долю от среднего (в %) составляет величина среднего квадратического отклонения - σ. P – точность опыта или относительная ошибка. t - критерий достоверности Стьюдента показывает во сколько раз величина среднего превосходит свою ошибку репрезентативности. t - это величина относительная, зависящая от численности выборки и заданной точности, требует сравнения с табличным значением (во всех учебниках статистики – Доспехова, Лакина). Для нашего числа наблюдений должна быть более 3. При полученном числе менее 3, необходимо увеличить число наблюдений. Но для малочисленной отобранной группы особей может быть и менее.
2. На следующем этапе вычисляется собственно селекционный дифференциал, как разность между средними значениями селектируемого признака в группе отобранных особей и в исходной популяции. Используем уже знакомый алгоритм.
Величину селекционного дифференциала выражают в натуральных величинах: размерных (м, см, кг, г, шт. и др.) или безразмерных (при относительных или производных признаках).
3. Для уточнения статистической достоверности разности между результатом отбора и среднепопуляционным значением признака используется формула достоверности разности двух средних:
где ν = Ne + Np – 2 = (Ne – 1) + (Np – 1) – число степеней свободы.
Если вычисленное значение t-критерия (опытное) больше его табличного значения для определенного числа степеней свободы и заданного уровня точности, то различия между средними можно признать достоверными. Об этом делают соответствующую запись в тетради. Такая ситуация в смысловом отношении означает то, что отбор действительно привел к изменению средних значений селектируемого признака, то, что величина полученного селекционного материала достоверно превышает среднее популяционное значение того же признака в исходной популяции, из которой был осуществлен отбор. Это соответствует тому, что разница между средними превышает величину случайных отклонений, не связанных с действием рассматриваемого фактора (в нашем случае с действием отбора). Это является подтверждением результативности отбора. Рассматриваемый показатель можно рассматривать как критерий достоверности селекционного дифференциала (В.П.).
4. При подтверждении достоверности селекционного дифференциала производят соответствующие вычисления его значения в относительных величинах: в % от среднего значения признака в исходной популяции. Используем формулу:
5. Вычисляют значения показателя интенсивности отбора, используя приведенные выше формулы.
Понятно, что полученная таким образом величина интенсивности отбора окажется относительной и при этом безразмерной.
6. интерпретируют весь полученный материал, о чем делают соответствующие записи.
|

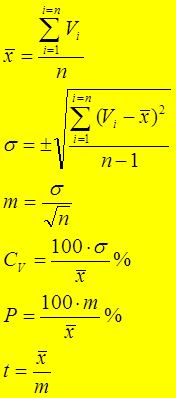
 - среднее значение признака в отобранной группе растений.
- среднее значение признака в отобранной группе растений.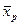 - среднее значение признака в популяции, из которой отобрана группа особей.
- среднее значение признака в популяции, из которой отобрана группа особей. ,
,  где
где - селекционный дифференциал;
- селекционный дифференциал;