Анализ содержания темы «Линии 2го порядка» в школьных учебниках по алгебре автора Ш. Ф. Алимова.
В 8 классе в §35на примере тела, брошенного вверх со скоростью v, выводится формула Начиная с §36, рассматривается функция 1. Проходит через начало координат 2. Симметричность относительно OY. 3. Вершина параболы 4. Убывание и возрастание на промежутках. 5. Фокус параболы (с ссылкой на рисунок) В конце параграфа представлена система заданий на усвоение и закрепление материала. Такие задания, как: 1. Построить график функции 2. При каких xзначения функции 3. Найти координаты точек пересечения Функция 1. Если a>0, то функция 2. Парабола симметрична относительно оси ординат 3. Если a>0, то функция Затем задается задача: На одной координатной плоскости построить графики функций Упражнения представлены в конце параграфа и содержат как легкие, так и повышенной сложности задания. Изучение графика функции Построить график функции 1. Вершина параболы 2. Ось симметрии параболы параллельна оси ординат и проходит через вершину параболы; 3. Направление ветвей параболы, если a>0- вверх, если a<0-вниз. Практическая часть разделена на уровни по сложности, каждый из уровней имеет по 6 заданий. Некоторые из них: 1) Найти координаты вершины параболы 2) Найти координаты точек пересечения параболы с осями координат: 3) Записать уравнение параболы, пересекающей ось абсцисс в точках x=-1 и x=3, а ось ординат в точке y=2. Функция 1) Область определения (-∞;0)˅(0;+∞); 2) нечетная, так как 3) убывает на промежутке x>0; 4) При x>0 функция принимает положительные значения; Затем говорится, что график функции Сразу дается на рассмотрение задача 2: Построить график функции Исследуя две функции поясняется, что функции симметричны относительно оси абсцисс. Функция
|

 , и дается определение квадратичной функции.
, и дается определение квадратичной функции. , найти значение yпри
, найти значение yпри  и т.д.;
и т.д.;
 рассматривается в 8 классе в § 37. Изучение сразу начинается с построения графика функции
рассматривается в 8 классе в § 37. Изучение сразу начинается с построения графика функции  и
и  с помощью таблицы значений. Сравнивая графики, делается вывод о том, что каждую точку графика функции
с помощью таблицы значений. Сравнивая графики, делается вывод о том, что каждую точку графика функции  можно получить из точки графика функции
можно получить из точки графика функции  с той же абсциссой увеличением её ординаты в 2 раза. Далее дается определение функции
с той же абсциссой увеличением её ординаты в 2 раза. Далее дается определение функции  принимает положительные значения, если a<0-отрицательные. И если значение функции
принимает положительные значения, если a<0-отрицательные. И если значение функции  и
и  . С помощью этих графиков решить неравенство
. С помощью этих графиков решить неравенство  .
.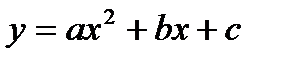 начинается с §38, где сразу дается задание:
начинается с §38, где сразу дается задание: и сравнить его с графиком функции
и сравнить его с графиком функции  . После проведенных рассуждений делается заключение, что графиком функции
. После проведенных рассуждений делается заключение, что графиком функции  вдоль координатных осей. И перечисляются свойства:
вдоль координатных осей. И перечисляются свойства: , где
, где  ;
; .
. .
. изучается в 9 классе, начиная с §15. Изучение начинается с задания: Построить график функции
изучается в 9 классе, начиная с §15. Изучение начинается с задания: Построить график функции  . И по графику начинается изучение свойств:
. И по графику начинается изучение свойств: при
при  .
. называется гиперболой, а две части, из которых она состоит, называются ветвями гиперболы.
называется гиперболой, а две части, из которых она состоит, называются ветвями гиперболы. соотносится с функцией
соотносится с функцией  обладает теми же свойствами, что и
обладает теми же свойствами, что и  при k>0 выражает обратную пропорциональную зависимость между x и y. И приводится пример из физики. Далее следует практическая часть, состоящая по сложности из уровней. Каждый из уровней содержат по четыре задачи на закрепление.
при k>0 выражает обратную пропорциональную зависимость между x и y. И приводится пример из физики. Далее следует практическая часть, состоящая по сложности из уровней. Каждый из уровней содержат по четыре задачи на закрепление.


