Анализ содержания темы «Линии 2го порядка» в школьных учебниках по алгебре А. Г. Мордковича
Изучение функции
Вводится понятие таблица значений, а затем полученные координаты строятся в прямоугольной системе координат. И сразу же говорится, что построенная линия называется параболой. Далее перечисляются геометрические свойства параболы: 1. симметричность относительно оси OY; 2. дается определение ветвей параболы; 3. вершина и её координаты; 4. наибольшее и наименьшее функции; 5. Убывание, возрастание; 6. Фокус параболы. Построение функции Весь материал представлен параллельно с примерами и изображенными графиками функций. Функция 1. Область определения функции (-∞;+∞); 2. y=0 при x=0;y>0 при x≠0; 3. Непрерывна; 4. yнаим=0 при x=0, yнаиб– не существует; 5. 6. 7. Область значений функции 8. Функция выпукла вниз. И при a<0 с непосредственной опорой на геометрическую модель-параболу. После теоретической части идут непосредственно, задания на усвоение: 1) Найти наиб. И наим. Значения функции 2) Решить уравнение Задания на закрепление, охватывают всю теоретическую часть и представлены в большом количестве. Здесь приведены задания на построение функции как в явной форме, так и построение линии по заданным значениям, свойствам. Также имеются задания на исследование уже построенных функций по рисункам. В 8 классе с § 37 изучается функция При этом дается задание: Не выполняя построения графика функции 1. Какая прямая служит осью параболы? 2. Каковы координаты вершины параболы? 3. Куда направлены ветви параболы? После построения графика данной функции вводится алгоритм построения параболы Практическая часть содержит большой объем заданий: легких, средней сложности и повышенной сложности. В 8 классе в § 18 Мордкович предлогает познакомимся с функцией 1) Гипербола симметрична относительно центра; 2) Имеет две асимптоты: ось x и ось y; 3) Имеет оси симметрии: y=x и y=-x. Затем дается пример: Найти наименьшее и наибольшее значение функции Далее вводится определение графика функции И поясняется, что две величины x и y обратно пропорциональны, если они связаны отношением xy=k (где k – число, отличное от нуля) Дальше автор по отдельности выделяет свойства функции Практическая часть для закрепления и усвоения данного материала содержит большое количество заданий трех уровней сложности. При этом это задачи как на построение графика функции, так и на исследование его свойств по строящимся чертежам, так и по готовым рисункам.
|

 начинается в 7 классе с § 37, где переход от линейной функции к квадратичной осуществляется на примере. (пусть x – сторона квадрата, y – его площадь, то
начинается в 7 классе с § 37, где переход от линейной функции к квадратичной осуществляется на примере. (пусть x – сторона квадрата, y – его площадь, то  и
и  , сравнивание, и анализ графика.
, сравнивание, и анализ графика. рассматривается в 8 классе в 3-ей главе § 17. И здесь говориться о том, что функция
рассматривается в 8 классе в 3-ей главе § 17. И здесь говориться о том, что функция 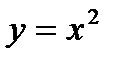 при a=1. Затем рассматриваются функции,
при a=1. Затем рассматриваются функции,  и
и  , составляется таблица значений, строятся графики (наглядность построения) и сравниваются. Затем идет пояснение, что каждая линия- парабола, а осьy–ось симметрии. Далее рассматривается случай при a=-1, выполняется построение графика, и делается вывод о направлении ветвей параболы. После чего дается определение функции
, составляется таблица значений, строятся графики (наглядность построения) и сравниваются. Затем идет пояснение, что каждая линия- парабола, а осьy–ось симметрии. Далее рассматривается случай при a=-1, выполняется построение графика, и делается вывод о направлении ветвей параболы. После чего дается определение функции  на отрезках: [0;2], [-2;-1], [-1;1,5].
на отрезках: [0;2], [-2;-1], [-1;1,5]. и другие.
и другие. и её свойства. Изучение начинается с рассмотрения многочлена
и её свойства. Изучение начинается с рассмотрения многочлена  , где a,b,c-числа, причем a≠0. И поясняется, что это квадратичный трехчлен. Затем рассматривается функция
, где a,b,c-числа, причем a≠0. И поясняется, что это квадратичный трехчлен. Затем рассматривается функция  и делается обобщение, что эти функции являются квадратичными. Автор предлагает рассмотреть квадратный трехчлен
и делается обобщение, что эти функции являются квадратичными. Автор предлагает рассмотреть квадратный трехчлен  , где
, где  . Затем вводится формула
. Затем вводится формула  и поясняется, что это формула для вычисления вершины параболы.
и поясняется, что это формула для вычисления вершины параболы. , ответить на следующие вопросы:
, ответить на следующие вопросы: .
. , где коэффициент k может принимать любые значения, кроме k=0. И предлагается рассмотреть функцию при k=1, составляется таблица значений при x>0, и строится график функции
, где коэффициент k может принимать любые значения, кроме k=0. И предлагается рассмотреть функцию при k=1, составляется таблица значений при x>0, и строится график функции  , а затем при x<0. Дальше говориться, что этот график функции
, а затем при x<0. Дальше говориться, что этот график функции  : на отрезке [1/2;4], на полуинтервале [-8;-1] и подробно расписывается ход действий.
: на отрезке [1/2;4], на полуинтервале [-8;-1] и подробно расписывается ход действий. .
.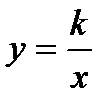 при k>0 и при k<0. Для усвоения изученного материала предлагается решить уравнение
при k>0 и при k<0. Для усвоения изученного материала предлагается решить уравнение 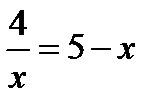 .
.


