Построение проекций цилиндра.

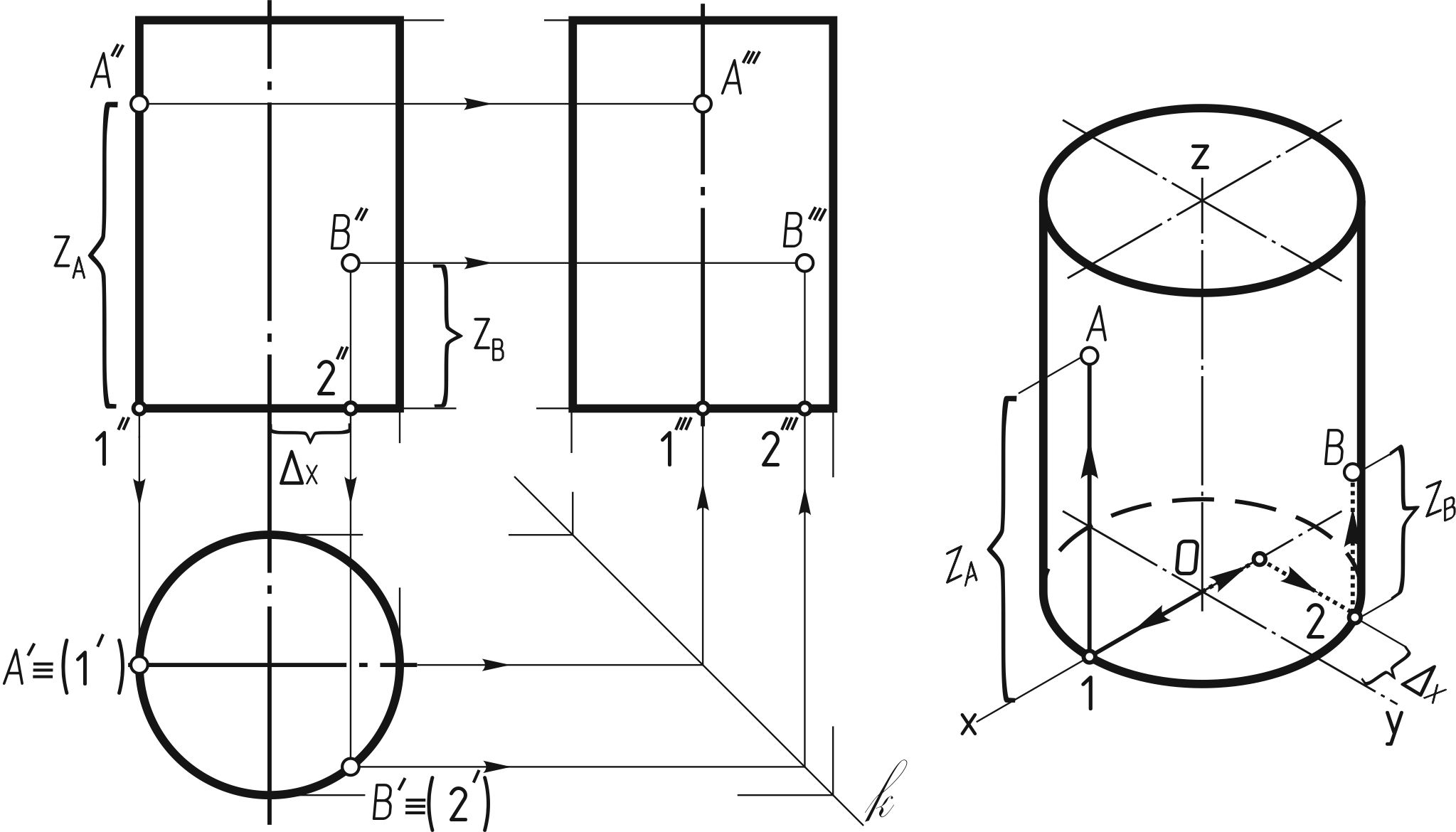
Построение горизонтальной и фронтальной проекций цилиндра начинают с изображения основания цилиндра, т. е. двух проекций окружности (см. рисунок 135, б). Так как окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой линии, равный диаметру окружности основания.

После построения основания на фронтальной проекции проводят две очерковые образующие (крайние образующие) и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра (рисунок 135, в).

Определение недостающих проекций точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном случае затруднений не вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рисунок 137, а). Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек A'' и B'' вертикальные линии связи до их пересечения с окружностью в искомых точках A' и B'.

Профильные проекции точек А и В строят также при помощи вертикальных и горизонтальных линий связи.

Изометрическую проекцию цилиндра вычерчивают, как показано на рисунок 137, б.

В изометрии точки А и В строят по их координатам. Например, для построения точки В от начала координат О по оси x откладывают координату ∆x, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 2. Из этой точки параллельно оси z проводят прямую, на которой откладывают координату Z_B, точки В.

 

 

а б

Рисунок 137

 

Прямой круговой конус. Прямым круговым конусом (рисунок 138) называют тело, ограниченное конической поверхностью вращения и кругом, расположенным в плоскости, перпендикулярной к оси конуса. Коническая поверхность получается при вращении прямолинейной образующей SA (рисунок 138, а), проходящей через неподвижную точку S на оси вращения i и составляющей с этой осью некоторый постоянный угол. Точка S называется вершиной конуса, а коническая поверхность — боковой поверхностью конуса. Размер прямого кругового конуса характеризуют диаметр его основания D_K и высота Н.

а) б) в)

Рисунок 138

 

Прямой круговой конус можно также рассматривать как тело, полученное при вращении прямоугольного треугольника SAB вокруг его катета SB (рисунок 139). При таком вращении гипотенуза описывает коническую поверхность, а катет АВ — круг, т. е. основание конуса.

 

Рисунок 139