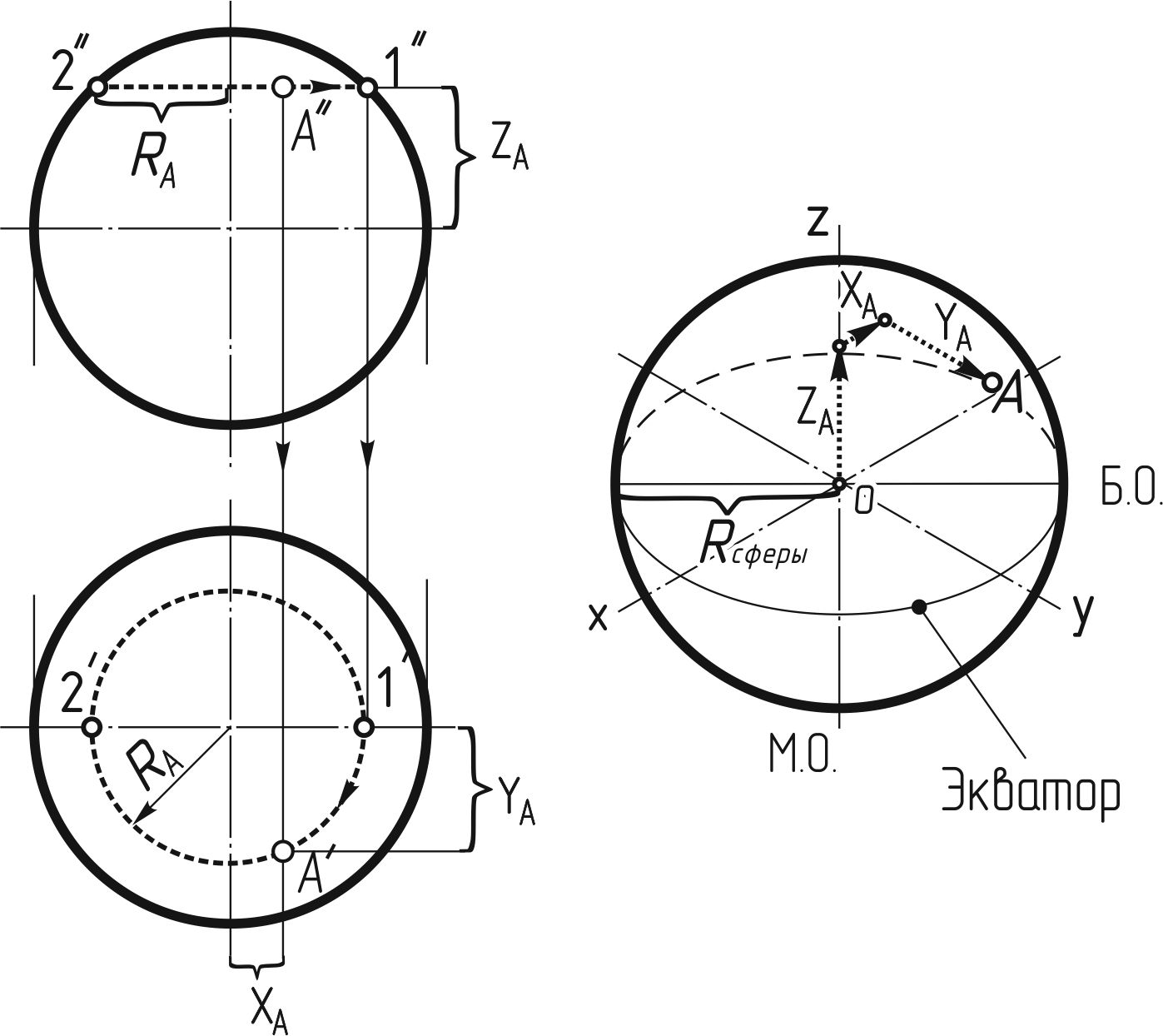
Построение проекций шара и точек на его поверхности
Проекции шара приведены на рисунке 142, а. Горизонтальная и фронтальная проекции — окружности радиуса, равного радиусу сферы.
а б Рисунок 142
Если точка А расположена на сферической поверхности, то вспомогательная линия 1'' 2'', проведенная через эту точку параллельно оси Ох (параллель), проецируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспомогательной окружности находят с помощью линии связи искомую горизонтальную проекцию A' точки А. Величина диаметра вспомогательной окружности равна фронтальной проекции 1''2''. Аксонометрическое изображениесферы (шара) выполняется в виде окружности (рисунок 142 б), радиус которой геометрически определяется как расстояние от центра сферы до проекции экватора (эллипса) вдоль большей ее оси (перпендикулярной Oz). В аксонометрической проекции точку А, находящуюся на поверхности шара, строят по трем координатам: XА, YА и ZА. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата XА; из конца ее параллельно оси у проведена прямая, на которой отложена координата YА; из конца отрезка, параллельно оси z проведена прямая, на которой отложена координата ZА. В результате построений получим искомую точку А. Тор – тело (рисунок 143), образованное вращением окружности или ее дуги вокруг оси, расположенной в одной с ней плоскости но не проходящей через центр окружности или ее дуги.
а б
Рисунок 143
Если ось вращения не пересекает образующую окружность, то тор называют кольцом (открытый тор) (рисунок 143, а). Если же ось вращения пересекает образующую окружность, то получается торовая поверхность бочкообразном формы (закрытый тор или пересекающийся тор) (рисунок 143, б). В последнем случае образующей торовой поверхности является дуга ABC окружности. Наибольшую из окружностей, которые описывают точки образующей торовой поверхности, называют экватором, а наименьшую — горлом, или горловиной.
|