Из ограничения D.90) вытекает еще один интересный результат. Если размер
скрытого слоя выбирается по следующей формуле (т.е. риск  минимизируется по
минимизируется по  ):
):
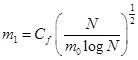
то риск  ограничивается величиной
ограничивается величиной 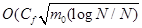 . Неожиданный аспект
. Неожиданный аспект
этого результата состоит в том, что в терминах поведения риска  скорость
скорость
сходимости, представленная как функция от размера обучающего множества  , имеет порядок (умноженный на логарифмический член). В то же время обычная гладкая функция (например, тригонометрическая или полиномиальная) демонстрирует несколько другое поведение. Пусть
, имеет порядок (умноженный на логарифмический член). В то же время обычная гладкая функция (например, тригонометрическая или полиномиальная) демонстрирует несколько другое поведение. Пусть 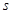 — мера гладкости, определяемая как степень дифференцируемости функции (количество существующих производных). Тогда для обычной гладкой функции минимаксная скорость сходимости общего риска
— мера гладкости, определяемая как степень дифференцируемости функции (количество существующих производных). Тогда для обычной гладкой функции минимаксная скорость сходимости общего риска  имеет порядок
имеет порядок 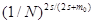 . Зависимость этой скорости от размерности входного пространства
. Зависимость этой скорости от размерности входного пространства  называют "проклятием размерности" (curse of dimensionality), поскольку это свойство ограничивает практическое использование таких функций. Таким образом, использование многослойного персептрона для решения задач аппроксимации обеспечивает определенные преимущества перед обычными гладкими функциями. Однако это преимущество появляется при условии, что первый абсолютный момент
называют "проклятием размерности" (curse of dimensionality), поскольку это свойство ограничивает практическое использование таких функций. Таким образом, использование многослойного персептрона для решения задач аппроксимации обеспечивает определенные преимущества перед обычными гладкими функциями. Однако это преимущество появляется при условии, что первый абсолютный момент  остается конечным. В этом состоит ограничение гладкости. Термин "проклятие размерности" (curse of dimensionality) был введен Ричардом Белманом (Richard Belman) в 1961 году в работе, посвященной процессам адаптивного управления. Если функция
остается конечным. В этом состоит ограничение гладкости. Термин "проклятие размерности" (curse of dimensionality) был введен Ричардом Белманом (Richard Belman) в 1961 году в работе, посвященной процессам адаптивного управления. Если функция 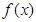 достаточно сложна и (по большей части) абсолютно неизвестна, необходимо уплотнить точки данных для более полного изучения поверхности. К сожалению, в многомерном пространстве из-за "проклятия размерности" очень сложно найти обучающую выборку с высокой плотностью дискретизации. В частности, в результате увеличения размерности наблюдается экспоненциальный рост сложности, что, в свою очередь, приводит к ухудшению пространственных свойств случайных точек с равномерным распределением. Функция, определенная в пространстве большой размерности, скорее всего, является значительно более сложной, чем функция, определенная в пространстве меньшей размерности, и эту сложность трудно разглядеть. Единственной возможностью избежать "проклятия размерности" является получение корректных априорных знаний о функции, определяемой данными обучения. Можно утверждать, что для практического получения хорошей оценки в пространствах высокой размерности необходимо обеспечить возрастание гладкости неизвестной функции наряду с увеличением размерности входных данных.
достаточно сложна и (по большей части) абсолютно неизвестна, необходимо уплотнить точки данных для более полного изучения поверхности. К сожалению, в многомерном пространстве из-за "проклятия размерности" очень сложно найти обучающую выборку с высокой плотностью дискретизации. В частности, в результате увеличения размерности наблюдается экспоненциальный рост сложности, что, в свою очередь, приводит к ухудшению пространственных свойств случайных точек с равномерным распределением. Функция, определенная в пространстве большой размерности, скорее всего, является значительно более сложной, чем функция, определенная в пространстве меньшей размерности, и эту сложность трудно разглядеть. Единственной возможностью избежать "проклятия размерности" является получение корректных априорных знаний о функции, определяемой данными обучения. Можно утверждать, что для практического получения хорошей оценки в пространствах высокой размерности необходимо обеспечить возрастание гладкости неизвестной функции наряду с увеличением размерности входных данных.

 минимизируется по
минимизируется по  ):
):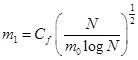
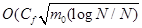 . Неожиданный аспект
. Неожиданный аспект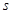 — мера гладкости, определяемая как степень дифференцируемости функции (количество существующих производных). Тогда для обычной гладкой функции минимаксная скорость сходимости общего риска
— мера гладкости, определяемая как степень дифференцируемости функции (количество существующих производных). Тогда для обычной гладкой функции минимаксная скорость сходимости общего риска 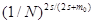 . Зависимость этой скорости от размерности входного пространства
. Зависимость этой скорости от размерности входного пространства  называют "проклятием размерности" (curse of dimensionality), поскольку это свойство ограничивает практическое использование таких функций. Таким образом, использование многослойного персептрона для решения задач аппроксимации обеспечивает определенные преимущества перед обычными гладкими функциями. Однако это преимущество появляется при условии, что первый абсолютный момент
называют "проклятием размерности" (curse of dimensionality), поскольку это свойство ограничивает практическое использование таких функций. Таким образом, использование многослойного персептрона для решения задач аппроксимации обеспечивает определенные преимущества перед обычными гладкими функциями. Однако это преимущество появляется при условии, что первый абсолютный момент  остается конечным. В этом состоит ограничение гладкости. Термин "проклятие размерности" (curse of dimensionality) был введен Ричардом Белманом (Richard Belman) в 1961 году в работе, посвященной процессам адаптивного управления. Если функция
остается конечным. В этом состоит ограничение гладкости. Термин "проклятие размерности" (curse of dimensionality) был введен Ричардом Белманом (Richard Belman) в 1961 году в работе, посвященной процессам адаптивного управления. Если функция 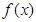 достаточно сложна и (по большей части) абсолютно неизвестна, необходимо уплотнить точки данных для более полного изучения поверхности. К сожалению, в многомерном пространстве из-за "проклятия размерности" очень сложно найти обучающую выборку с высокой плотностью дискретизации. В частности, в результате увеличения размерности наблюдается экспоненциальный рост сложности, что, в свою очередь, приводит к ухудшению пространственных свойств случайных точек с равномерным распределением. Функция, определенная в пространстве большой размерности, скорее всего, является значительно более сложной, чем функция, определенная в пространстве меньшей размерности, и эту сложность трудно разглядеть. Единственной возможностью избежать "проклятия размерности" является получение корректных априорных знаний о функции, определяемой данными обучения. Можно утверждать, что для практического получения хорошей оценки в пространствах высокой размерности необходимо обеспечить возрастание гладкости неизвестной функции наряду с увеличением размерности входных данных.
достаточно сложна и (по большей части) абсолютно неизвестна, необходимо уплотнить точки данных для более полного изучения поверхности. К сожалению, в многомерном пространстве из-за "проклятия размерности" очень сложно найти обучающую выборку с высокой плотностью дискретизации. В частности, в результате увеличения размерности наблюдается экспоненциальный рост сложности, что, в свою очередь, приводит к ухудшению пространственных свойств случайных точек с равномерным распределением. Функция, определенная в пространстве большой размерности, скорее всего, является значительно более сложной, чем функция, определенная в пространстве меньшей размерности, и эту сложность трудно разглядеть. Единственной возможностью избежать "проклятия размерности" является получение корректных априорных знаний о функции, определяемой данными обучения. Можно утверждать, что для практического получения хорошей оценки в пространствах высокой размерности необходимо обеспечить возрастание гладкости неизвестной функции наряду с увеличением размерности входных данных.


