В [96] были исследованы аппроксимирующие свойства многослойного персептрона для случая одного скрытого слоя с сигмоидальной функцией активации и одного линейного выходного нейрона. Эта сеть обучалась с помощью алгоритма обратного распространения, после чего тестировалась на новых данных. Во время обучения сети предъявлялись выбранные точки аппроксимируемой функции  , в результате чего была получена аппроксимирующая функция
, в результате чего была получена аппроксимирующая функция  , определяемая выражением D.86). Если сети предъявлялись не использованные ранее данные, то функция
, определяемая выражением D.86). Если сети предъявлялись не использованные ранее данные, то функция  "оценивала" новые точки целевой функции, т.е.
"оценивала" новые точки целевой функции, т.е.  .
.
Гладкость целевой функции  выражалась в терминах ее разложения Фурье. В частности, в качестве предельной амплитуды функции
выражалась в терминах ее разложения Фурье. В частности, в качестве предельной амплитуды функции  использовалось среднее значение нормы вектора частоты, взвешенного значениями амплитуды распределения Фурье.
использовалось среднее значение нормы вектора частоты, взвешенного значениями амплитуды распределения Фурье.
Пусть 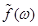 — многомерное преобразование Фурье функции
— многомерное преобразование Фурье функции  , где
, где
 — вектор частоты. Функция
— вектор частоты. Функция  , представленная в терминах преобразования Фурье
, представленная в терминах преобразования Фурье 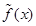 , определяется следующей инверсной формулой:
, определяется следующей инверсной формулой:
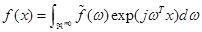
где  . Для комплекснозначной функции
. Для комплекснозначной функции 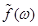 с интегрируемой функцией
с интегрируемой функцией  первый абсолютный момент распределения Фурье функции можно определить следующим образом:
первый абсолютный момент распределения Фурье функции можно определить следующим образом:
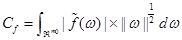
где  — Евклидова норма вектора
— Евклидова норма вектора  ;
;  — абсолютное значение функции
— абсолютное значение функции  .
.
Первый абсолютный момент  является мерой гладкости (smoothness) функции
является мерой гладкости (smoothness) функции  . Первый абсолютный момент
. Первый абсолютный момент  является основой для вычисления пределов ошибки, которая возникает вследствие использования многослойного персептрона, представленного функцией отображения «вход-выход»
является основой для вычисления пределов ошибки, которая возникает вследствие использования многослойного персептрона, представленного функцией отображения «вход-выход»  , аппроксимирующей функцию
, аппроксимирующей функцию  . Ошибка аппроксимации измеряется интегральной квадратичной ошибкой по произвольной мере вероятности
. Ошибка аппроксимации измеряется интегральной квадратичной ошибкой по произвольной мере вероятности  для шара
для шара  радиуса
радиуса  . На этом основании можно сформулировать следующее утверждение для предела ошибки аппроксимации.
. На этом основании можно сформулировать следующее утверждение для предела ошибки аппроксимации.
Для любой непрерывной функции  с конечным первым моментом
с конечным первым моментом  и любого
и любого  существует некоторая линейная комбинация сигмоидальных функций
существует некоторая линейная комбинация сигмоидальных функций  вида D.86), такая, что
вида D.86), такая, что  где
где  .
.
Если функция  наблюдается на множестве значений
наблюдается на множестве значений 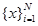 входного вектора
входного вектора
х, принадлежащего шару  , этот результат определяет следующее ограничение для эмпирического риска:
, этот результат определяет следующее ограничение для эмпирического риска:

В [95] результат D.89) использовался для описания границ риска  ,
,
возникающего при использовании многослойного персептрона с  входными узлами и
входными узлами и  скрытыми нейронами:
скрытыми нейронами:
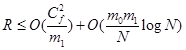
Два слагаемых в этом определении границ риска  отражают компромисс между двумя противоречивыми требованиями к размеру скрытого слоя.
отражают компромисс между двумя противоречивыми требованиями к размеру скрытого слоя.
1. Точность наилучшей аппроксимации (accuracy of the best approximation). В
соответствии с теоремой об универсальной аппроксимации для удовлетворения этого
требования размер скрытого слоя  должен быть большим.
должен быть большим.
2. Точность эмпирического соответствия аппроксимации. Для того чтобы удовлетворить этому требованию, отношение  должно иметь малое значение. Для фиксированного объема
должно иметь малое значение. Для фиксированного объема  обучающего множества размер скрытого слоя
обучающего множества размер скрытого слоя  должен оставаться малым, что противоречит первому требованию. Ограничение для риска
должен оставаться малым, что противоречит первому требованию. Ограничение для риска  , описанное формулой D.90), имеет еще одно интересное применение. Дело в том, что для точной оценки целевой функции не требуется экспоненциально большого обучающего множества и большой размерности входного пространства
, описанное формулой D.90), имеет еще одно интересное применение. Дело в том, что для точной оценки целевой функции не требуется экспоненциально большого обучающего множества и большой размерности входного пространства  , если первый абсолютный момент
, если первый абсолютный момент  остается конечным. Это еще больше повышает практическую ценность многослойного персептрона, используемого в качестве универсального аппроксиматора. Ошибку между эмпирическим соответствием и наилучшей аппроксимацией можно рассматривать как ошибку оценивания. Пусть
остается конечным. Это еще больше повышает практическую ценность многослойного персептрона, используемого в качестве универсального аппроксиматора. Ошибку между эмпирическим соответствием и наилучшей аппроксимацией можно рассматривать как ошибку оценивания. Пусть  — среднеквадратическое значение ошибки оценивания. Можно сделать вывод, что размер
— среднеквадратическое значение ошибки оценивания. Можно сделать вывод, что размер  обучающего множества, необходимый для хорошего обобщения, должен иметь порядок
обучающего множества, необходимый для хорошего обобщения, должен иметь порядок  . Математическая структура этого результата аналогична эмпирическому правилу D.85, если произведение
. Математическая структура этого результата аналогична эмпирическому правилу D.85, если произведение  соответствует общему количеству свободных параметров
соответствует общему количеству свободных параметров  сети. Другими словами можно утверждать, что для хорошего качества аппроксимации размер обучающего множества должен превышать отношение общего количества свободных параметров сети к среднеквадратическому значению ошибки оценивания.
сети. Другими словами можно утверждать, что для хорошего качества аппроксимации размер обучающего множества должен превышать отношение общего количества свободных параметров сети к среднеквадратическому значению ошибки оценивания.

 , в результате чего была получена аппроксимирующая функция
, в результате чего была получена аппроксимирующая функция  , определяемая выражением D.86). Если сети предъявлялись не использованные ранее данные, то функция
, определяемая выражением D.86). Если сети предъявлялись не использованные ранее данные, то функция  .
.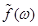 — многомерное преобразование Фурье функции
— многомерное преобразование Фурье функции  , где
, где — вектор частоты. Функция
— вектор частоты. Функция  , представленная в терминах преобразования Фурье
, представленная в терминах преобразования Фурье 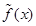 , определяется следующей инверсной формулой:
, определяется следующей инверсной формулой: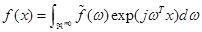
 . Для комплекснозначной функции
. Для комплекснозначной функции  первый абсолютный момент распределения Фурье функции можно определить следующим образом:
первый абсолютный момент распределения Фурье функции можно определить следующим образом: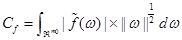
 — Евклидова норма вектора
— Евклидова норма вектора  — абсолютное значение функции
— абсолютное значение функции  .
. является мерой гладкости (smoothness) функции
является мерой гладкости (smoothness) функции  , аппроксимирующей функцию
, аппроксимирующей функцию  для шара
для шара  радиуса
радиуса  . На этом основании можно сформулировать следующее утверждение для предела ошибки аппроксимации.
. На этом основании можно сформулировать следующее утверждение для предела ошибки аппроксимации. существует некоторая линейная комбинация сигмоидальных функций
существует некоторая линейная комбинация сигмоидальных функций  где
где  .
.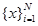 входного вектора
входного вектора , этот результат определяет следующее ограничение для эмпирического риска:
, этот результат определяет следующее ограничение для эмпирического риска:
 ,
, входными узлами и
входными узлами и  скрытыми нейронами:
скрытыми нейронами: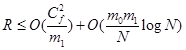
 должен быть большим.
должен быть большим. должно иметь малое значение. Для фиксированного объема
должно иметь малое значение. Для фиксированного объема  обучающего множества размер скрытого слоя
обучающего множества размер скрытого слоя  , если первый абсолютный момент
, если первый абсолютный момент  остается конечным. Это еще больше повышает практическую ценность многослойного персептрона, используемого в качестве универсального аппроксиматора. Ошибку между эмпирическим соответствием и наилучшей аппроксимацией можно рассматривать как ошибку оценивания. Пусть
остается конечным. Это еще больше повышает практическую ценность многослойного персептрона, используемого в качестве универсального аппроксиматора. Ошибку между эмпирическим соответствием и наилучшей аппроксимацией можно рассматривать как ошибку оценивания. Пусть  — среднеквадратическое значение ошибки оценивания. Можно сделать вывод, что размер
— среднеквадратическое значение ошибки оценивания. Можно сделать вывод, что размер  . Математическая структура этого результата аналогична эмпирическому правилу D.85, если произведение
. Математическая структура этого результата аналогична эмпирическому правилу D.85, если произведение  соответствует общему количеству свободных параметров
соответствует общему количеству свободных параметров  сети. Другими словами можно утверждать, что для хорошего качества аппроксимации размер обучающего множества должен превышать отношение общего количества свободных параметров сети к среднеквадратическому значению ошибки оценивания.
сети. Другими словами можно утверждать, что для хорошего качества аппроксимации размер обучающего множества должен превышать отношение общего количества свободных параметров сети к среднеквадратическому значению ошибки оценивания.


