Указания к решению задач. Задачи данного раздела рассчитаны на применение уравнения Бернулли для потока реальной жидкости (2.3)
Задачи данного раздела рассчитаны на применение уравнения Бернулли для потока реальной жидкости (2.3). Полагая при этом поток турбулентным, коэффициент Кориолиса можно принимать α = 1. При применении уравнения Бернулли важно правильно выбрать те два сечения, для которых оно записывается. В качестве сечений рекомендуется брать: - свободную поверхность жидкости в резервуаре (баке), где скорость потока v = 0; - выход в атмосферу, где р изб = 0; р абс = р атм; - сечение, где присоединен тот или иной манометр, пьезометр или вакуумметр; - неподвижный воздух вдалеке от входа в трубу, в которую происходит всасывание из атмосферы. Уравнение Бернулли рекомендуется сначала записать в общем виде, а затем переписать с заменой его членов заданными буквенными величинами и исключить члены, равные нулю. При этом необходимо помнить следующее: - вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх; - давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной); - суммарная потеря напора Σ h всегда пишется в правой части уравнения Бернулли со знаком «+»; - величина Σ h в общем случае складывается из местных потерь, которые можно выражать формулой Вейсбаха (2.4), и потерь на трение по длине, определяемых формулой Дарси (2.6).
Примеры решения задач
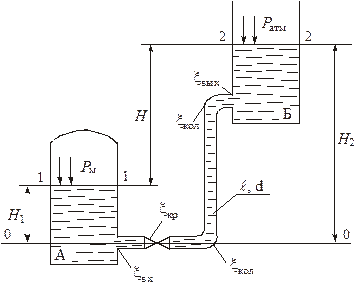 Пример 2.1. Из резервуара А, заполненного водой и находящегося под манометрическим давлением Рм = 0,5 атм, вода подается по стальному трубопроводу длиной l = 10 м и диаметром d = 100 мм в резервуар Б на высоту Н = 2 м. Коэффициент сопротивлений крана ξкр = 9, каждого колена ξкол =0,25; ξвх = 0,5; ξвых = 1. Коэффициент гидравлического трения λ = 0,04. Определить режим течения, расход Q и скорость V воды в трубопроводе. Пример 2.1. Из резервуара А, заполненного водой и находящегося под манометрическим давлением Рм = 0,5 атм, вода подается по стальному трубопроводу длиной l = 10 м и диаметром d = 100 мм в резервуар Б на высоту Н = 2 м. Коэффициент сопротивлений крана ξкр = 9, каждого колена ξкол =0,25; ξвх = 0,5; ξвых = 1. Коэффициент гидравлического трения λ = 0,04. Определить режим течения, расход Q и скорость V воды в трубопроводе.
Решение: Уравнение Бернулли в общем случае имеет вид:
Первое сечение (1-1) возьмем на свободной поверхности воды в баке А, второе (2-2) – на свободной поверхности в баке Б. Плоскость сравнения совместим с осью трубопровода в месте соединения его с баком А (см. рисунок). Давления в первом и втором сечениях возьмем абсолютные. Скоростью изменения уровней воды в баках А и Б можно пренебречь, поэтому в уравнении (2.9) v1 = v2 = 0. Тогда уравнение (2.9) примет вид
Отсюда (учитывая, что Н2 = Н1 + Н) получаем
Режим течения определим по значению числа Рейнольдса:
Т.к. Re > 2300, следовательно, режим турбулентный. Расход в трубе определится как
Решение: Удельный вес керосина γ = ρ · g = 800 · 10 = 8000 Н/м3. Поместим первое и второе поперечные сечения потока, а также плоскость сравнения так, как показано на рисунке. Тогда уравнение Бернулли примет вид:
или
Воспользоваться уравнением (2.10) мы не можем, т.к. нам неизвестно значение коэффициента гидравлического трения λ. Поэтому дальнейшее решение проводим методом последовательных приближений. 1-е приближение. Задаемся значением λ из диапазона 0,02…0,04. Пусть λ = 0,02. Тогда из (2.10) находим скорость:
Далее определяем число Рейнольдса:
Поскольку режим турбулентный, а труба гладкая – коэффициент гидравлического трения λ находим по формуле Блазиуса:
Различие между принятым и получившимся значениями λ составит
Поскольку разница превышает 5%, сделаем второе приближение. 2-е приближение. Пусть λ = 0,022. Тогда из (2.10)
Поскольку теперь λ = λ′, приближения заканчиваем. Расход теперь определится как
Данный метод позволяет с достаточной точностью производить инженерные расчеты.
ЗАДАЧИ К ГЛАВЕ 2
Определить расход Q жидкости и построить пьезометрическую и напорную линии.
|

 . (2.9)
. (2.9) .
. .
.
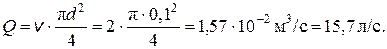

 Пример 2.2. Определить расход керосина, вытекающего из бака по трубопроводу длиной l = 10 м и диаметром d = 50 мм, если избыточное давление в баке Рм = 16 кПа, высота уровня Н1 = 1 м, высота подъема керосина в открытом пьезометре Н2 = 1,75 м. Труба гидравлически гладкая (шероховатость D = 0). Плотность керосина ρ = 800 кг/м3, кинематическая вязкость n = 0,025 см2/с.
Пример 2.2. Определить расход керосина, вытекающего из бака по трубопроводу длиной l = 10 м и диаметром d = 50 мм, если избыточное давление в баке Рм = 16 кПа, высота уровня Н1 = 1 м, высота подъема керосина в открытом пьезометре Н2 = 1,75 м. Труба гидравлически гладкая (шероховатость D = 0). Плотность керосина ρ = 800 кг/м3, кинематическая вязкость n = 0,025 см2/с.

 . (2.10)
. (2.10)
 .
.
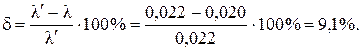





 Задача 27. Масло трансформаторное из большого резервуара, в котором поддерживается постоянный ее уровень, по стальному нержавеющему трубопроводу вытекает в атмосферу. Диаметр трубопровода d = 70 мм, его горизонтальная и наклонная части одинаковой длины l = 3,4 м. Высота уровня жидкости над горизонтальной частью трубопровода равна Н = 6,2 м, конец его наклонной части находится ниже горизонтальной части на величину h = 1,5 м. Плотность масла ρ = 900 кг/м3, кинематическая вязкость ν = 0,2 см2/с. Эквивалентная шероховатость трубопровода Δ = 0,1 мм.
Задача 27. Масло трансформаторное из большого резервуара, в котором поддерживается постоянный ее уровень, по стальному нержавеющему трубопроводу вытекает в атмосферу. Диаметр трубопровода d = 70 мм, его горизонтальная и наклонная части одинаковой длины l = 3,4 м. Высота уровня жидкости над горизонтальной частью трубопровода равна Н = 6,2 м, конец его наклонной части находится ниже горизонтальной части на величину h = 1,5 м. Плотность масла ρ = 900 кг/м3, кинематическая вязкость ν = 0,2 см2/с. Эквивалентная шероховатость трубопровода Δ = 0,1 мм.


