ГЛАВА 1. ГИДРОСТАТИКА
- молоко - хлеб - фрукты - фарш - квашеная капуста
10. Выберите вариант, при котором условия хранения не нарушены: - мясо при t -18° - 2 месяца - рыба при t -3° - 3 дня - фарш при t -4° - 36 часов - молоко при t -2° - 72 часа - колбаса при t -3° - 24 часа - сметана при t -4° - 6 дней ГЛАВА 1. ГИДРОСТАТИКА Давление в неподвижной жидкости называется гидростатическим и обладает следующими двумя свойствами: - на внешней поверхности жидкости оно всегда направлено по нормали внутрь объема жидкости; - в любой точке внутри жидкости оно по всем направлениям одинаково, т.е. не зависит от угла наклона площадки, по которой действует. Уравнение, выражающее гидростатическое давление р в любой точке неподвижной жидкости в том случае, когда из числа массовых сил на нее действует лишь одна сила тяжести, называется основным уравнением гидростатики: р = р 0 + h r g = р 0 + g h,(1.1) где р 0 - давление на какой-либо поверхности уровня жидкости, например, на свободной поверхности; h - глубина расположения рассматриваемой точки, отсчитанная от поверхности с давлением р 0. В тех случаях, когда рассматриваемая точка расположена выше поверхности с давлением р 0, второй член в формуле (1.1) отрицателен. Другая форма записи того же уравнения (1.1) имеет вид
где z и z 0 - вертикальные координаты произвольной точки и свободной поверхности, отсчитываемые от горизонтальной плоскости вверх; р/( r g) - пьезометрическая высота (если р – избыточное давление); р/( r g) - приведенная пьезометрическая высота (если р – абсолютное давление). Подавляющее большинство механизмов и сооружений работают при окружающем давлении, равном атмосферному. Наличие в устройстве жидкости или газа под избыточным (вакуумметрическим) давлением обусловливает возникновение в его деталях дополнительных напряжений, которые определяют прочность изделия, а также его работоспособность. Поэтому часто необходимо знать силу избыточного воздействия жидкости на устройство. Сила избыточного давления жидкости на плоскую стенку равна произведению гидростатического давления p Cв центре тяжести площади стенки на площадь стенки S, т. е. F = p C · S (1.2) Центр давления (точка приложения силы) расположен ниже центра тяжести площади или совпадает с последним в случае горизонтальной стенки. Расстояние между центром тяжести площади и центром давления в направлении нормали к линии пересечения плоскости стенки со свободной поверхностью жидкости равно
где I 0- момент инерции площади стенки относительно оси, проходящей через центр тяжести площади и параллельной линии пересечения плоскости стенки со свободной поверхностью; у С- координата центра тяжести площади. Сила давления жидкости на криволинейную стенку, симметричную относительно вертикальной плоскости, складывается из горизонтальной F x и вертикальной F z составляющих:
Горизонтальная составляющая F x равна силе давления жидкости на вертикальную проекцию данной стенки: F x = h Cr g S в. (1.5) Вертикальная составляющая F z равна весу тела давления, или другими словами, весу жидкости в объеме W, заключенном между данной стенкой, свободной поверхностью жидкости и вертикальной проецирующей поверхностью, проведенной по контуру стенки. Если избыточное давление Относительный покой жидкости - это равновесие ее в движущихся сосудах, когда помимо силы тяжести на жидкость действует вторая массовая сила - сила инерции переносного движения, причем эта сила постоянна по времени. Возможны два случая относительного покоя жидкости: в сосуде, движущемся прямолинейно и равноускоренно, ив сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью. В обоих случаях поверхности уровня, т. е. поверхности равного давления (в том числе и свободная поверхность жидкости) принимают такой вид, при котором равнодействующая массовая сила нормальна к этим поверхностям во всех их точках. В сосуде, движущемся прямолинейно и равноускоренно, поверхности уровня будут плоскими. В сосуде, равномерно вращающемся вокруг вертикальной оси, поверхности уровня представляют собой параболоиды вращения, ось которых совпадает с осью вращения сосуда. Уравнение поверхности уровня (в частности, свободной поверхности жидкости в открытом сосуде) в цилиндрических координатах (r, z) имеет вид
где z 0 - вертикальная координата вершины параболоида поверхности уровня; r, z - координаты любой точки поверхности уровня. Закон распределения давления по объему жидкости, вращающейся вместе с сосудом, выражается уравнением
где ρ0 - давление в точке с координатами r = 0, z = z0. Таким образом, повышение давления в жидкости, возникающее вследствие ее вращения, равно
что позволяет определить повышение давления в любой интересующей нас точке объема.
Указания к решению задач
При решении задач по гидростатике прежде всего нужно хорошо усвоить и не смешивать такие понятия, как давление р и сила F. При решении задач на определение давления в той или иной точке неподвижной жидкости следует пользоваться основным уравнением гидростатики (1.1). Применяя это уравнение, нужно иметь в виду, что второй член в правой части этого уравнения может быть как положительным, так и отрицательным. Очевидно, что при увеличении глубины давление возрастает, а при подъеме – уменьшается. Необходимо твердо различать давления абсолютное, избыточное и вакуум и обязательно знать связь между давлением, удельным весом и высотой, соответствующей этому давлению (пьезометрической высотой). При решении задач, в которых даны поршни или системы поршней, следует писать уравнение равновесия, т.е. равенство нулю суммы всех сил, действующих на поршень (систему поршней).
Примеры решения задач
Решение: Проведем плоскость равного давления (через нижний мениск бензина). Давления в левом и правом колене на этом уровне будут равны, т.е. можно записать согласно основному уравнению гидростатики: Ратм + gб · hб = Ратм + gв · hв Отсюда находим удельный вес бензина
или, учитывая, что g = r · g:
Ответ:
Пример 1.2. Определить объемный модуль упругости жидкости, если под действием груза А массой 250 кг поршень прошел расстояние Dh = 5 мм. Начальная высота положения поршня (без груза) Н = 1,5 м, диаметры поршня d = 80 мм и резервуара D = 300 мм, высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким.
Решение: Модуль объемной упругости К определяется выражением:
Изменение объема жидкости при этом произошло на величину
Учитывая, что начальный объем жидкости определяется как
величина, обратная относительному изменению объема, составит:
Окончательно модуль объемной упругости К составит: К = −0,5 · 106 · (−3696) = 1848 · 106 Па. Ответ: К = 1848 · 106 Па.
Пример 1.3. Плоский прямоугольный щит перекрывает выходное отверстие резервуара под углом α = 600. Щит имеет размеры a × b = 2 × 3 м, вес G = 5 кН. Глубина воды перед щитом h = 5 м. Удельный вес воды g = 104 Н/м3. Трением в шарнирах пренебречь. Определить начальную силу тяги Т троса, необходимую для открывания щита.
Решение: Из рисунка видно, что центр тяжести щита (точка С) находится на глубине
Найдем величину силы избыточного давления воды на затвор:
Приложена сила F в центре давления (точка D), положение которой определяется выражением (сравни с (1.3))
Находим
Окончательно для центра давления получим
Для определения силы натяжения троса Т покажем силы, действующие на затвор (см. рис.), и составим уравнение равновесия щита, т.е. сумма моментов действующих сил относительно оси шарнира должна быть равна нулю:
Отсюда находим
Пример 1.4. Определить усилие натяжения троса при подъеме полусферической крышки в сосуде, если высота уровня жидкости Н = 4 м; избыточное давление Рм = 2 атм; радиус крышки R = 1 м. Весом крышки пренебречь.
Решение: На крышку действуют две силы: сила натяжения троса Т и сила давления жидкости Fz = γ · Wт.д. Из условия равновесия крышки получаем, что Т = Fz = γ · Wт.д.
Окончательно для силы натяжения троса получим Т = 104 · 73,3 = 73,3 · 104 Н.
Пример 1.5. В сосуд высотой Н = 0,3 м залита жидкость до уровня h = 0,2 м. Определить, до какой угловой скорости ω можно раскрутить сосуд, с тем, чтобы жидкость не выплеснулась из него, если его диаметр D = 100 мм.
Решение: Ось z совместим с осью вращения, а ось r пустим по дну сосуда.
Здесь нам неизвестны z0 и ω. Учитывая, что z = H при r = D/2, получим
Исходный объем жидкости определится как
Объем параболоида можно определить как
Приравнивая объемы Wисх = Wпар, получаем
Приравнивая теперь (1.9) и (1.10), находим ω:
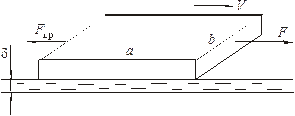
Пример 1.6. К прямоугольному бруску, скользящему по тонкому слою масла на горизонтальной поверхности, приложена сила F = 1 Н. Определить скорость установившегося движения бруска. Размеры бруска a × b = 0,2 × 0,1 м. Толщина слоя масла δ = 0,5 мм. Коэффициент динамической вязкости масла μ = 0,050 Па с.
Fтр = F. Учитывая, что слой масла тонкий, можно принять распределение скорости масла по толщине слоя линейным, т.е.
И тогда сила Fтр (по закону жидкостного трения Ньютона) определится как
Приравнивая Fтр и F, получаем
Пример 1.7. Герметично закрытая цистерна диаметром D = 3 м полностью заполнена керосином плотностью ρ = 830 кг/м3. Показание манометра Рм = 0,5 атм. Определить силу избыточного давления F керосина на торцевую крышку, а также найти координату приложения этой силы.
Удельный вес керосина имеет величину γ = ρ · g = 830 · 10 = 8300 Н/м3.
F = γ · hц.т. · S. Поскольку на свободной поверхности имеется избыточное давление, ее нужно поднять на высоту Рм/γ (рисунок 1.7а) так, что (см. рисунок 1.7б)
Таким образом
Положение центра давления определяется величиной lц.д.:
Ответ: F = 441 кН, ℓц.д = 7,59 м.
ЗАДАЧИ К ГЛАВЕ 1
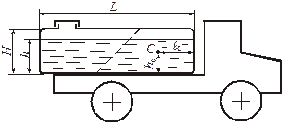 Задача 11. Определить расположение центра тяжести С бетонного раствора (hС и lС), залитого в закрытый кузов автомобиля при его торможении с ускорением а = g. Считать, что кузов имеет форму параллелепипеда: L = 1,92 м, H = 1,2 м и h = 1 м. Задача 11. Определить расположение центра тяжести С бетонного раствора (hС и lС), залитого в закрытый кузов автомобиля при его торможении с ускорением а = g. Считать, что кузов имеет форму параллелепипеда: L = 1,92 м, H = 1,2 м и h = 1 м.

|

 ,
, , (1.3)
, (1.3) . (1.4)
. (1.4) на свободной поверхности жидкости отлично от нуля, то при расчете следует эту поверхность мысленно поднять (или опустить) на высоту (пьезометрическую высоту)
на свободной поверхности жидкости отлично от нуля, то при расчете следует эту поверхность мысленно поднять (или опустить) на высоту (пьезометрическую высоту)  , (1.6)
, (1.6) , (1.7)
, (1.7) , (1.8)
, (1.8) Пример 1.1. В U-образную трубку налиты вода и бензин. Определить плотность бензина, если hб = 500 мм; hв = 350 мм. Капиллярный эффект не учитывать.
Пример 1.1. В U-образную трубку налиты вода и бензин. Определить плотность бензина, если hб = 500 мм; hв = 350 мм. Капиллярный эффект не учитывать.

 .
. .
. .
.
 .
. Приложение груза вызвало повышение давления на величину:
Приложение груза вызвало повышение давления на величину: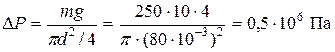 .
. .
. ,
,




 .
.
 Учитывая, что момент инерции прямоугольника равен
Учитывая, что момент инерции прямоугольника равен  , площадь S = a · b, отрезок CD (эксцентриситет е) определится как
, площадь S = a · b, отрезок CD (эксцентриситет е) определится как .
. lц.д. = 4,77 + 0, 07 = 4,84 м.
lц.д. = 4,77 + 0, 07 = 4,84 м.


 Поскольку на свободной поверхности жидкости действует избыточное давление, для определения объема тела давления Wт.д. необходимо сначала поднять свободную поверхность на высоту
Поскольку на свободной поверхности жидкости действует избыточное давление, для определения объема тела давления Wт.д. необходимо сначала поднять свободную поверхность на высоту  . Тогда объем тела давления определится как разность объемов цилиндра и полусферы:
. Тогда объем тела давления определится как разность объемов цилиндра и полусферы:
 Свободная поверхность жидкости во вращающемся сосуде описывается уравнением (1.6)
Свободная поверхность жидкости во вращающемся сосуде описывается уравнением (1.6) .
. , или
, или  (1.9)
(1.9) Второе уравнение, связывающее z0 и ω, получим, приравняв объемы жидкости в исходном, статичном и рабочем состояниях.
Второе уравнение, связывающее z0 и ω, получим, приравняв объемы жидкости в исходном, статичном и рабочем состояниях. .
.
 (1.10)
(1.10)
 Решение:
Решение: При установившемся движении бруска (ускорение равно нулю) проекция равнодействующей силы на горизонтальную ось равна нулю, т.е.
При установившемся движении бруска (ускорение равно нулю) проекция равнодействующей силы на горизонтальную ось равна нулю, т.е.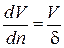 .
.

 Решение:
Решение: Сила избыточного давления жидкости на плоскую поверхность определяется как
Сила избыточного давления жидкости на плоскую поверхность определяется как

 Поскольку днище расположено вертикально, hц.т. = lц.т.
Поскольку днище расположено вертикально, hц.т. = lц.т.
 Учитывая, что момент инерции круга
Учитывая, что момент инерции круга  , получим
, получим



 Задача 19. Круглое отверстие между двумя резервуарами закрыто конической крышкой с размерами D = 550 мм и L = 450 мм. Закрытый резервуар заполнен водой, а открытый резервуар – глицерином. К закрытому резервуару сверху присоединен
Задача 19. Круглое отверстие между двумя резервуарами закрыто конической крышкой с размерами D = 550 мм и L = 450 мм. Закрытый резервуар заполнен водой, а открытый резервуар – глицерином. К закрытому резервуару сверху присоединен


