ГЛАВА 2. ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ
При решении некоторых простейших задач о движении жидкостей часто в первом приближении делают допущение о том, что движущаяся жидкость является идеальной. Под идеальной понимают жидкость абсолютно несжимаемую и нерасширяемую, не способную сопротивляться растяжению и сдвигу, а также лишенную свойства испаряемости (р н.п = 0). Главное, чем отличается жидкость идеальная от жидкости реальной, - это отсутствие у нее вязкости, вызывающей способность сопротивления сдвигу, т. е. возникновению касательных напряжений (трения в жидкости). Следовательно, в движущейся идеальной жидкости возможен лишь один вид напряжений - напряжение сжатия, т. е. давление р, а касательное напряжение τ = 0. Основными уравнениями, позволяющими решать простейшие задачи о движении идеальной жидкости, является уравнение расхода и уравнение Бернулли. Уравнение расхода представляет собой условие неразрывности (сплошности) потока несжимаемой жидкости, или, что то же самое, равенство объемных расходов в каких-то двух поперечных сечениях одного и того же потока, например 1 и 2, т. е. Q 1 = Q 2 или v 1 S 1 = v 2 S 2. Отсюда следует, что
т. е. скорости обратно пропорциональны площадям поперечных сечений потоков. При этом предполагается, что скорость во всех точках данного сечения одинакова. Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения удельной энергии жидкости вдоль потока. Под удельной понимают энергию, отнесенную к единице веса, объема или массы жидкости. Обычно удобнее бывает относить энергию к единице веса. В этом случае уравнение Бернулли, записанное для сечений 1 и 2 элементарной струйки или потока идеальной жидкости, имеет вид
где z - вертикальные координаты центров тяжести сечений или удельная энергия положения; р /(ρ g) - пьезометрическая (приведенная пьезометрическая) высота, или удельная энергия давления; v 2/(2 g) - скоростной напор, или удельная кинетическая энергия; Н - полный напор, или полная удельная энергия жидкости. Для потока реальной (вязкой) жидкости уравнение Бернулли следует писать в таком виде:
где v ср - средняя по сечению скорость, равная v ср = Q / S; α - коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям и равный отношению действительной кинетической энергии потока к кинетической энергии того же потока, но при равномерном распределении скоростей; Σ h - суммарная потеря полного напора между сечениями 1 и 2, обусловленная вязкостью жидкости. Различают два вида гидравлических потерь напора: местные потери и потери на трение по длине. Местные потери напора происходят в так называемых местных гидравлических сопротивлениях, т. е. в местах изменения формы и размеров русла, где поток так или иначе деформируется - расширяется, сужается, искривляется - или имеет место более сложная деформация. Местные потери выражают формулой Вейсбаха
где v - средняя скорость потока в сечении перед местным сопротивлением (при расширении) или за ним (при сужении) и в тех случаях, когда рассматривают потери напора в гидроарматуре различного назначения; ζм - безразмерный коэффициент местного сопротивления.
Числовое значение коэффициента в основном определяется формой местного сопротивления, его геометрическими параметрами, но иногда влияет также число Рейнольдса, которое для труб диаметром d выражается формулой
здесь n - кинематическая вязкость жидкости, выражаемая в м2/с или см2/с. Число Рейнольдса определяет режим движения жидкостей (и газов) в трубах. При Re < Reкр, где Reкр ≈ 2300, режим движения ламинарный, т.е. слоистый - без перемешивания жидкости и без пульсаций скоростей и давлений. При Re > Reкр режим течения турбулентный, т.е. с перемешиванием жидкости и с пульсациями скоростей и давлений. Потери напора на трение по длине l определяются общей формулой Дарси
где безразмерный коэффициент сопротивления трения l определяется в зависимости от режима течения: при ламинарном режиме lл однозначно определяется число Рейнольдса, т.е.
при турбулентном режиме lт помимо числа Рейнольдса зависит еще от относительной шероховатости D/ d, т.е., используя формулу Альтшуля
где Δ – высота микронеровностей стенки трубы (эквивалентная шероховатость), мм.
|

 , (2.1)
, (2.1)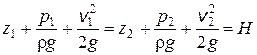 , (2.2)
, (2.2)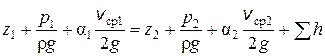 , (2.3)
, (2.3)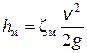 , (2.4)
, (2.4)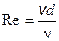 , (2.5)
, (2.5)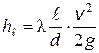 , (2.6)
, (2.6) ; (2.7)
; (2.7)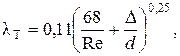 (2.8)
(2.8)


