Указания к решению задач
Задачи данного раздела можно решать без записи уравнения Бернулли. Так, если дана задача на истечение через отверстие, насадок или дроссель (жиклер) и задан коэффициент расхода, то следует применить основное выражение (3.5). При этом следует помнить, что расчетный напор в общем случае складывается из разностей геометрических и пьезометрических высот (3.2). Следует знать, что коэффициент расхода μ однозначно определяется коэффициентами сжатия струи ε и скорости φ (или сопротивления ζ). Указанное выше основное выражение для расхода справедливо и при истечении через отверстия, насадки и дроссели в среду, заполненную той же самой жидкостью (истечение под уровень). При этом кинетическая энергия, теряемая на вихреобразования, учитывается коэффициентом расхода. Если истечение жидкости происходит при переменном напоре (опорожнение резервуаров), то в каждый данный момент движение жидкости можно рассматривать как установившееся.
Примеры решения задач
Пример 3.1. Определить направление истечения воды через отверстие диаметром d = 5 мм и расход, если разность уровней Н = 2 м, показание вакуумметра Рвак соответствует 147 мм рт. ст., показание манометра Рм = 0,25 МПа, коэффициент расхода μ = 0,62. Удельные веса ртути и воды принять γрт = 13,6 · 104 Н/м3; γ = 104 Н/м3.
Для определения расхода воспользуемся формулой (3.5):
Учитывая, что Р1 = Ратм – Рвак; Р2 = Ратм + Рм; Н1 – Н2 = Н; получим
Поскольку в задаче вакуум задан высотой ртутного столба, выразим необходимое нам вакуумметрическое давление Рвак как Рвак = γрт · hрт, и тогда окончательно для расчетного напора получим:
Так как Нрасч отрицательный, истечение будет происходить в направлении, противоположном принятому, т.е. справа налево.
ЗАДАЧИ К ГЛАВЕ 3
У к а з а н и е: площадь дросселирующего кольца определить по приближенной формуле S = Sо – Sи, где Sо – площадь отверстия, Sи – площадь иглы в сечении 1–1.
|

 Решение:
Решение:
 Расчетный напор определяется разностью полных напоров до отверстия и после него. Поскольку направление истечения нам неизвестно, допустим, что оно происходит слева направо (см. рис.). Обозначив абсолютные давления над жидкостью слева Р1, справа Р2, глубины погружения Н1 и Н2, для Нрасч получим (сравни с формулой 3.2)
Расчетный напор определяется разностью полных напоров до отверстия и после него. Поскольку направление истечения нам неизвестно, допустим, что оно происходит слева направо (см. рис.). Обозначив абсолютные давления над жидкостью слева Р1, справа Р2, глубины погружения Н1 и Н2, для Нрасч получим (сравни с формулой 3.2)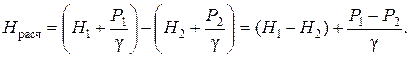


 Расход при этом определится как
Расход при этом определится как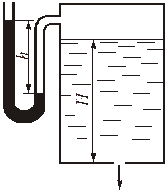

 Задача 37. На рисунке изображена схема регулируемого игольчатого дросселя. Определить, на какое расстояние l необходимо вдвинуть иглу в дросселирующее отверстие для обеспечения перепада давления Δр = р1 – р2 = 3 МПа, если угол иглы α = 30о, диаметр дросселирующего отверстия D = 6 мм, его коэффициент расхода μ = 0,8, расход жидкости Q = 1,2 л/с, плотность рабочей жидкости ρ = 900 кг/м3.
Задача 37. На рисунке изображена схема регулируемого игольчатого дросселя. Определить, на какое расстояние l необходимо вдвинуть иглу в дросселирующее отверстие для обеспечения перепада давления Δр = р1 – р2 = 3 МПа, если угол иглы α = 30о, диаметр дросселирующего отверстия D = 6 мм, его коэффициент расхода μ = 0,8, расход жидкости Q = 1,2 л/с, плотность рабочей жидкости ρ = 900 кг/м3.


