Любая линейная комбинация собственных векторов, соответствующих одному тому же собственному числу  , является собственным вектором, относящимся к тому же собственному числу
, является собственным вектором, относящимся к тому же собственному числу  . Отсюда следует, то все собственные векторы, соответствующие одному и тому же числу
. Отсюда следует, то все собственные векторы, соответствующие одному и тому же числу  , образуют линейное пространство, которое является подпространством в
, образуют линейное пространство, которое является подпространством в 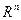 .
.
Докажем теорему о том, что собственные векторы, соответствующие различным собственным числам, образуют линейно независимую систему.
Пусть  . Предположим (от противного), что
. Предположим (от противного), что  - линейно зависимая система, это означает, что векторы коллинеарны:
- линейно зависимая система, это означает, что векторы коллинеарны:  .
.
С одной стороны, 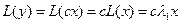 , но то же время
, но то же время  . Получается, что
. Получается, что  , то есть
, то есть 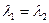 , что противоречит тому, что собственные числа различны. Итак, предположение коллинеарности собственных векторов, относящихся различным собственным числам, было неверно, значит эти векторы образуют линейно- независимую систему, что и требовалось доказать. Аналогично проводится доказательство для системы из n векторов. Если система
, что противоречит тому, что собственные числа различны. Итак, предположение коллинеарности собственных векторов, относящихся различным собственным числам, было неверно, значит эти векторы образуют линейно- независимую систему, что и требовалось доказать. Аналогично проводится доказательство для системы из n векторов. Если система  собственных векторов, относящихся соответственно к
собственных векторов, относящихся соответственно к  , является линейно зависимой, то один из векторов системы является линейной комбинацией остальных. Положим для определённости
, является линейно зависимой, то один из векторов системы является линейной комбинацией остальных. Положим для определённости  . Тогда:
. Тогда:
 , но в то же время
, но в то же время  . Тогда разность:
. Тогда разность:
 , что означало бы
, что означало бы  для всех индексов i. Но по условию, собственные числа различны. Получили противоречие. Следовательно, система векторов
для всех индексов i. Но по условию, собственные числа различны. Получили противоречие. Следовательно, система векторов  линейно независима.
линейно независима.
Ядро линейного оператора. Ядром линейного оператора  называется совокупность всех векторов пространства, для которых
называется совокупность всех векторов пространства, для которых  . Легко доказывается, что все такие векторы образуют подпространство:
. Легко доказывается, что все такие векторы образуют подпространство:
 ,то есть линейная комбинация векторов принадлежащих ядру оператора, тоже принадлежит ядру. Очевидно, ядро является собственным подпространством, соответствующим числу
,то есть линейная комбинация векторов принадлежащих ядру оператора, тоже принадлежит ядру. Очевидно, ядро является собственным подпространством, соответствующим числу  .
.
Докажем, что если существует хотя бы один ненулевой вектор, отображаемый линейным оператором в 0, то этот оператор не будет обратимым.
Пусть  , то есть вектор принадлежит ядру оператора. Тогда для матрицы этого оператора верно
, то есть вектор принадлежит ядру оператора. Тогда для матрицы этого оператора верно 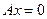 , то есть однородная система
, то есть однородная система
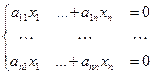
имеет нетривиальное решение. Отсюда следует, что матрица А (а это одновременно и основная матрица данной системы уравнений, и матрица линейного оператора) является вырожденной, то есть не существует обратной матрицы, следовательно, для оператора  не существует обратный оператор
не существует обратный оператор  .
.

 , является собственным вектором, относящимся к тому же собственному числу
, является собственным вектором, относящимся к тому же собственному числу 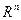 .
. . Предположим (от противного), что
. Предположим (от противного), что  - линейно зависимая система, это означает, что векторы коллинеарны:
- линейно зависимая система, это означает, что векторы коллинеарны:  .
.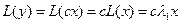 , но то же время
, но то же время  . Получается, что
. Получается, что  , то есть
, то есть 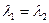 , что противоречит тому, что собственные числа различны. Итак, предположение коллинеарности собственных векторов, относящихся различным собственным числам, было неверно, значит эти векторы образуют линейно- независимую систему, что и требовалось доказать. Аналогично проводится доказательство для системы из n векторов. Если система
, что противоречит тому, что собственные числа различны. Итак, предположение коллинеарности собственных векторов, относящихся различным собственным числам, было неверно, значит эти векторы образуют линейно- независимую систему, что и требовалось доказать. Аналогично проводится доказательство для системы из n векторов. Если система  собственных векторов, относящихся соответственно к
собственных векторов, относящихся соответственно к  , является линейно зависимой, то один из векторов системы является линейной комбинацией остальных. Положим для определённости
, является линейно зависимой, то один из векторов системы является линейной комбинацией остальных. Положим для определённости  . Тогда:
. Тогда: , но в то же время
, но в то же время  . Тогда разность:
. Тогда разность: , что означало бы
, что означало бы  для всех индексов i. Но по условию, собственные числа различны. Получили противоречие. Следовательно, система векторов
для всех индексов i. Но по условию, собственные числа различны. Получили противоречие. Следовательно, система векторов  называется совокупность всех векторов пространства, для которых
называется совокупность всех векторов пространства, для которых  . Легко доказывается, что все такие векторы образуют подпространство:
. Легко доказывается, что все такие векторы образуют подпространство: ,то есть линейная комбинация векторов принадлежащих ядру оператора, тоже принадлежит ядру. Очевидно, ядро является собственным подпространством, соответствующим числу
,то есть линейная комбинация векторов принадлежащих ядру оператора, тоже принадлежит ядру. Очевидно, ядро является собственным подпространством, соответствующим числу  .
.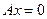 , то есть однородная система
, то есть однородная система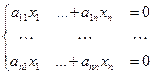
 .
.


