Построение матрицы линейного оператора.
2.1. Построение матрицы по заданной формуле отображения. Пусть отображение задано с помощью формулы
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор Пример 1. Пусть оператор задан с помощью формулы:
Прежде всего, докажем, что это отображение – действительно л инейный оператор. Отобразим сумму векторов:
Аналогично для умножения на константу:
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1=1, x2=0, а затем x1=0, x2=1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1). Поэтому матрица линейного оператора будет иметь вид:
Аналогичным способом решается задача и для 3 и большего количества переменных. Пример 2. Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3). Матрица линейного оператора:
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается. Если задана система Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений. Пусть Пример. Найти матрицу линейного оператора, отображающего базис
Здесь
Проверка осуществляется умножением получившейся матрицы на каждый вектор: Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач. 2.3. Прочие способы нахождения матрицы оператора. Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2. Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида Аналогично,
Координаты полученных векторов запишем в виде столбцов матрицы оператора. Матрица оператора: Аналогично можно построить матрицу линейного оператора
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n+1. Возьмём в качестве базиса элементы
Матрица этого линейного оператора:
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
|

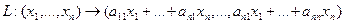
 , найдём его образ, это будет вектор
, найдём его образ, это будет вектор  . Для этого в формуле, задающей образ вектора, полагаем
. Для этого в формуле, задающей образ вектора, полагаем 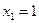 ,
,  ,…,
,…,  . Аналогично находим образы для
. Аналогично находим образы для  ,…,
,…,  . Из координат образа вектора
. Из координат образа вектора  составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.
составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.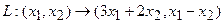 .
.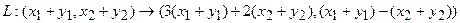 Теперь каждую координату получившегося вектора можем преобразовать:
Теперь каждую координату получившегося вектора можем преобразовать:


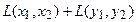 .
.
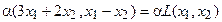
 .
.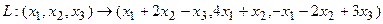 .
. .
.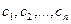 из n векторов, образующих базис, и какая-нибудь произвольная система n векторов
из n векторов, образующих базис, и какая-нибудь произвольная система n векторов  (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.
(возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.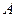 - матрица оператора в базисе
- матрица оператора в базисе 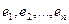 . По условию,
. По условию, 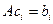 для всех индексов
для всех индексов  . Данные n равенств можно записать в виде одного матричного равенства:
. Данные n равенств можно записать в виде одного матричного равенства:  , при этом столбцы матрицы
, при этом столбцы матрицы  - это векторы
- это векторы  - векторы
- векторы  .
. в систему векторов
в систему векторов  .
. ,
,  ,
, 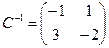 , и получаем:
, и получаем: .
. .
. и
и  . Построим матрицу одного из этих операторов,
. Построим матрицу одного из этих операторов,  .
.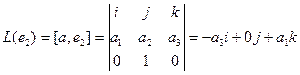 ,
, .
. .
. .
. ,
, 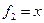 ,
,  ,…,
,…, 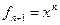 .
.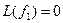 ,
,  ,
,  , аналогично получим
, аналогично получим 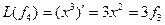 ,…,
,…, 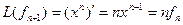 .
.



