Определение. Ненулевой вектор  называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , соответствующим собственному числу
, соответствующим собственному числу  , если выполнено равенство
, если выполнено равенство  .
.
Замечание. Если рассматривать нулевой вектор, то он был бы собственным для любого числа  , потому что
, потому что  . Таким образом, в определении вектор 0 исключается из рассмотрения, однако 0-вектор включается в собственное подпространство (п.3.3.).
. Таким образом, в определении вектор 0 исключается из рассмотрения, однако 0-вектор включается в собственное подпространство (п.3.3.).
Определение. Пусть 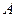 - матрица линейного оператора
- матрица линейного оператора  . Матрица
. Матрица 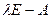 называется характеристической матрицей линейного оператора, уравнение
называется характеристической матрицей линейного оператора, уравнение 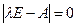 - характеристическим уравнением, а его корни – характеристическим корнями линейного оператора.
- характеристическим уравнением, а его корни – характеристическим корнями линейного оператора.
Докажем, что любое собственное число является характеристическим корнем.
Пусть  - собственное число, то есть для некоторого вектора
- собственное число, то есть для некоторого вектора  выполняется
выполняется  . Запишем это равенство подробнее:
. Запишем это равенство подробнее:
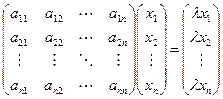
Умножаем матрицу на вектор, и затем в получившейся системе уравнений переносим все слагаемые в правую часть. Получается однородная система уравнений, которую можно записать в виде:
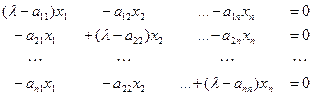
Основная матрица этой системы – матрица 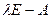 . Для однородной системы существует нетривиальное решение тогда и только тогда, когда её матрица вырождена, таким образом,
. Для однородной системы существует нетривиальное решение тогда и только тогда, когда её матрица вырождена, таким образом, 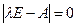 , то есть, если
, то есть, если  - собственный вектор, то число
- собственный вектор, то число  является характеристическим корнем.
является характеристическим корнем.
Алгоритм нахождения собственных чисел и собственных векторов.
1) Найти корни характеристического уравнения 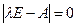 .
.
Замечание. Можно также найти корни уравнения  , но в этом случае при нечётном порядке матрицы, коэффициент при
, но в этом случае при нечётном порядке матрицы, коэффициент при  будет отрицательный.
будет отрицательный.
2) Для каждого найденного характеристического корня решить однородную систему 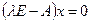 и найти её фундаментальную систему решений (это и будут собственные векторы, соответствующие данному числу
и найти её фундаментальную систему решений (это и будут собственные векторы, соответствующие данному числу  ). При изучении линейной алгебры наиболее часто рассматривают собственные числа и векторы для операторов в
). При изучении линейной алгебры наиболее часто рассматривают собственные числа и векторы для операторов в  . В этом случае характеристическое уравнение будет третьей степени. Можно найти 3 корня с помощью теоремы Виета, либо найти их поочерёдно следующим способом. Допустим, нам известен один характеристический корень
. В этом случае характеристическое уравнение будет третьей степени. Можно найти 3 корня с помощью теоремы Виета, либо найти их поочерёдно следующим способом. Допустим, нам известен один характеристический корень  , тогда можем поделить характеристический многочлен на
, тогда можем поделить характеристический многочлен на 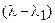 , причём деление будет без остатка, так как
, причём деление будет без остатка, так как  - корень многочлена. Частное – многочлен степени 2, в свою очередь его 2 корня легко могут быть найдены через дискриминант. Для нахождения какого-либо одного корня уравнения третьего порядка можно применять следующее утверждение из общей алгебры:
- корень многочлена. Частное – многочлен степени 2, в свою очередь его 2 корня легко могут быть найдены через дискриминант. Для нахождения какого-либо одного корня уравнения третьего порядка можно применять следующее утверждение из общей алгебры:
Если число  – рациональный корень многочлена с целыми коэффициентами
– рациональный корень многочлена с целыми коэффициентами  , то коэффициент
, то коэффициент 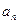 делится на
делится на  ,
, 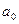 делится на
делится на  .
.
Доказательство. Если  - корень, то
- корень, то 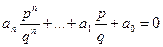 , умножим равенство на
, умножим равенство на  : получаем
: получаем  , следовательно,
, следовательно,  . Правая часть этого равенства делится на
. Правая часть этого равенства делится на  , поэтому левая часть тоже делится на
, поэтому левая часть тоже делится на  , то есть
, то есть 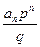 – целое число, но так как
– целое число, но так как  и
и  взаимно простые числа, то
взаимно простые числа, то 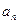 делится на
делится на  . Аналогично,
. Аналогично,  делится на
делится на  , так как
, так как 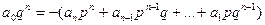 , откуда следует что
, откуда следует что 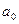 делится на
делится на  .
.
Таким образом, можно легко установить конечное множество возможных рациональных, в том числе целых, корней многочлена, и найти все корни, проводя проверку чисел из этого множества.

 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , соответствующим собственному числу
, соответствующим собственному числу  , если выполнено равенство
, если выполнено равенство  .
. . Таким образом, в определении вектор 0 исключается из рассмотрения, однако 0-вектор включается в собственное подпространство (п.3.3.).
. Таким образом, в определении вектор 0 исключается из рассмотрения, однако 0-вектор включается в собственное подпространство (п.3.3.).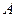 - матрица линейного оператора
- матрица линейного оператора  . Матрица
. Матрица 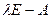 называется характеристической матрицей линейного оператора, уравнение
называется характеристической матрицей линейного оператора, уравнение 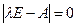 - характеристическим уравнением, а его корни – характеристическим корнями линейного оператора.
- характеристическим уравнением, а его корни – характеристическим корнями линейного оператора.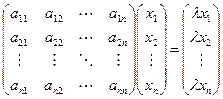
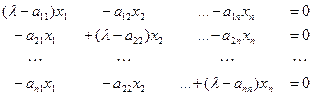
 , но в этом случае при нечётном порядке матрицы, коэффициент при
, но в этом случае при нечётном порядке матрицы, коэффициент при  будет отрицательный.
будет отрицательный.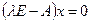 и найти её фундаментальную систему решений (это и будут собственные векторы, соответствующие данному числу
и найти её фундаментальную систему решений (это и будут собственные векторы, соответствующие данному числу  . В этом случае характеристическое уравнение будет третьей степени. Можно найти 3 корня с помощью теоремы Виета, либо найти их поочерёдно следующим способом. Допустим, нам известен один характеристический корень
. В этом случае характеристическое уравнение будет третьей степени. Можно найти 3 корня с помощью теоремы Виета, либо найти их поочерёдно следующим способом. Допустим, нам известен один характеристический корень  , тогда можем поделить характеристический многочлен на
, тогда можем поделить характеристический многочлен на 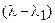 , причём деление будет без остатка, так как
, причём деление будет без остатка, так как  – рациональный корень многочлена с целыми коэффициентами
– рациональный корень многочлена с целыми коэффициентами  , то коэффициент
, то коэффициент 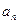 делится на
делится на  ,
, 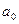 делится на
делится на  .
.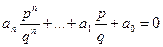 , умножим равенство на
, умножим равенство на  : получаем
: получаем  , следовательно,
, следовательно,  . Правая часть этого равенства делится на
. Правая часть этого равенства делится на 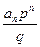 – целое число, но так как
– целое число, но так как  делится на
делится на 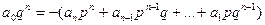 , откуда следует что
, откуда следует что 


