Определение. Билинейной формой на пространстве 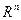 называется отображение
называется отображение  , сопоставляющее каждой паре векторов число, причём:
, сопоставляющее каждой паре векторов число, причём:
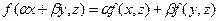
 .
.
Всякую билинейную форму можно задать с помощью матрицы:
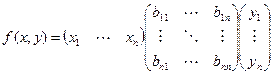
То есть,  .
.
Замечание. Обычное скалярное произведение также является билинейной формой и соответствует единичной матрице  .
.
Если положить  для билинейной формы, то полученное отображение
для билинейной формы, то полученное отображение  называется квадратичной формой на пространстве
называется квадратичной формой на пространстве 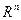 . Квадратичная форма имеет вид
. Квадратичная форма имеет вид  . Поскольку
. Поскольку  , то на значение квадратичной формы влияют только суммы вида
, то на значение квадратичной формы влияют только суммы вида  , а не каждое слагаемое в отдельности. Отсюда очевидно, что квадратичную форму всегда можно задать с помощью симметрической матрицы.
, а не каждое слагаемое в отдельности. Отсюда очевидно, что квадратичную форму всегда можно задать с помощью симметрической матрицы.
Если квадратичная форма имеет вид  , то она называется квадратичной формой в каноническом виде.
, то она называется квадратичной формой в каноническом виде.
Теорема. Любую квадратичную форму в 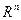 можно привести к каноническому виду с помощью перехода к новому базису.
можно привести к каноническому виду с помощью перехода к новому базису.
Доказательство. Для симметрического оператора всегда существует n собственных чисел, и, соответственно, n собственных векторов. Отсюда следует, что в новом базисе, составленном из этих собственных векторов, матрица оператора будет диагональной. Такое свойство базиса, состоящего из собственных векторов симметрического оператора, позволяет применять симметрические операторы к преобразованию квадратичных форм. Ведь всякая квадратичная форма задаётся симметрической матрицей, значит, её матрица может быть преобразована к диагональному виду. Это означает, что в новом базисе квадратичная форма не будет содержать произведений различных переменных, а будет состоять только из вторых степеней переменных.
Алгоритм приведения квадратичной формы к главным осям:
1) Построить матрицу квадратичной формы.
2) Найти собственные числа и векторы, записать квадратичную форму (коэффициентами при квадратах новых переменных будут найденные собственные числа).
3) Нормировать собственные векторы и записать матрицу перехода от старого базиса к новому (а именно, состоящему из найденных векторов).
Пример 1. привести к главным осям квадратичную форму третьего порядка.
 .
.
Построим матрицу этой квадратичной формы:
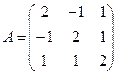
Найдём собственные числа и векторы:  . Простому корню 0 соответствует собственный вектор
. Простому корню 0 соответствует собственный вектор 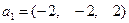 , кратному корню 3 соответствуют два собственных вектора:
, кратному корню 3 соответствуют два собственных вектора: 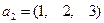 ,
,  . Запишем матрицу перехода, предварительно поделив каждый вектор на его модуль.
. Запишем матрицу перехода, предварительно поделив каждый вектор на его модуль.
 ,
,
а квадратичная форма имеет вид: 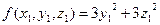 .
.
Пример 2. (с дробными коэффициентами квадратичной формы). Привести к главным осям квадратичную форму третьего порядка.
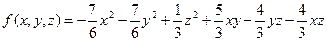
Решение. Сначала построим матрицу квадратичной формы.

Найдём 3 собственных числа. λ = 1, -1, -2. Затем для каждого собственного числа найдём собственный вектор и нормируем его.
λ =1 x= 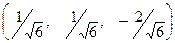
λ =-1 x=  .
.
λ =-2 x= 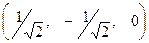
Квадратичная форма в новом базисе: 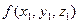 =
=  .
.
§ 5. Приложения. Задачи для самостоятельного решения и самопроверки.
В задачах 1 – 90 все 3 характеристических корня различны, в задачах 91 – 150 есть корень кратности 2.
5.1. найти матрицу линейного оператора, отображающего систему векторов
a1, a2, a3 в систему векторов b1, b2, b3.
| Вариант 1
a1=(0 -4 -1) b1=(16 -8 6)
a2=(1 -5 -5) b2=(21 -22 15)
a3=(2 4 1) b3=(-14 14 -6)
Вариант 2
a1=(1 3 2) b1=(13 16 1)
a2=(4 0 5) b2=(1 16 4)
a3=(4 4 5) b3=(17 32 0)
Вариант 3
a1=(2 -1 0) b1=(3 -4 4)
a2=(4 -2 -3) b2=(12 -5 17)
a3=(5 -5 0) b3=(0 -5 0)
Вариант 4
a1=(3 2 -3) b1=(-11 5 15)
a2=(0 -1 -1) b2=(1 -4 -1)
a3=(0 -2 -4) b3=(-4 -14 2)
Вариант 5
a1=(-1 2 -2) b1=(-4 -5 2)
a2=(-1 -4 1) b2=(23 -5 -19)
a3=(3 -5 -3) b3=(16 -2 -11)
Вариант 6
a1=(-4 -2 -2) b1=(-4 18 -32)
a2=(2 -4 -3) b2=(11 3 -11)
a3=(0 3 3) b3=(-6 -9 18)
Вариант 7
a1=(1 -5 2) b1=(-29 -31 14)
a2=(4 5 1) b2=(5 8 -22)
a3=(-4 -2 -5) b3=(19 11 0)
Вариант 8
a1=(-3 3 -2) b1=(12 -11 -3)
a2=(2 -4 2) b2=(-20 16 10)
a3=(3 -3 3) b3=(-15 15 3)
Вариант 9
a1=(4 5 -3) b1=(-19 -17 18)
a2=(-1 4 -1) b2=(-4 6 20)
a3=(0 -5 3) b3=(11 -3 -26)
| Вариант 10
a1=(-1 1 4) b1=(-4 21 5)
a2=(1 1 -1) b2=(8 -5 6)
a3=(-4 -4 4) b3=(-32 20 -24)
Вариант 11
a1=(2 1 -2) b1=(3 -12 9)
a2=(2 -4 2) b2=(-14 -16 8)
a3=(-2 -1 -3) b3=(-13 -8 11)
Вариант 12
a1=(0 -3 4) b1=(-21 6 -25)
a2=(-3 -3 0) b2=(-9 -21 6)
a3=(1 0 4) b3=(-12 17 -21)
Вариант 13
a1=(2 3 4) b1=(1 18 2)
a2=(3 -5 2) b2=(-27 11 -1)
a3=(4 1 -2) b3=(-13 -4 -6)
Вариант 14
a1=(-3 1 1) b1=(-12 -2 -8)
a2=(3 0 0) b2=(9 3 15)
a3=(3 -5 -5) b3=(24 -2 -20)
Вариант 15
a1=(-3 -2 -4) b1=(32 9 -7)
a2=(0 3 1) b2=(-15 -1 14)
a3=(5 4 0) b3=(-36 -29 1)
Вариант 16
a1=(-4 -5 -3) b1=(2 17 -24)
a2=(-1 2 -4) b2=(-6 1 -6)
a3=(2 2 0) b3=(0 -4 6)
Вариант 17
a1=(2 -1 2) b1=(-11 -5 -9)
a2=(-1 2 4) b2=(5 -4 -10)
a3=(0 1 0) b3=(3 -1 -3)
Вариант 18
a1=(0 0 3) b1=(3 -3 -3)
a2=(-3 0 -1) b2=(-10 -2 -8)
a3=(-1 -3 -1) b3=(-10 -3 4)
|
5.2. найти все собственные числа и собственные векторы для оператора.
Задачи 1-90: все характеристические корни различны.
| Вариант 1
9 8 -4
-4 -3 2
5 7 0
Вариант 2
7 1 -13
-4 1 10
2 1 -2
Вариант 3
4 1 1
-1 0 -1
-1 1 2
Вариант 4
1 -1 -1
4 6 5
-2 -2 -1
Вариант 5
-3 -10 -6
1 4 1
2 4 5
Вариант 6
-3 -5 -6
2 4 2
2 2 5
Вариант 7
4 4 3
-3 -3 -3
2 4 5
Вариант 8
4 -4 -6
3 -3 -6
-1 2 5
Вариант 9
5 2 2
-8 -4 -6
4 3 5
Вариант 10
1 -4 0
1 4 1
0 2 1
| Вариант 11
2 3 -1
1 -4 1
5 -33 8
Вариант 12
10 3 8
-24 -5 -24
-1 -1 1
Вариант 13
2 -1 0
-6 3 2
3 -3 1
Вариант 14
3 -2 2
-2 3 0
-3 3 0
Вариант 15
-2 -1 4
-4 1 4
-5 -1 7
Вариант 16
5 -6 2
6 -11 4
15 -33 12
Вариант 17
2 -4 -2
-1 -3 -2
2 12 7
Вариант 18
13 18 -4
-7 -10 2
9 15 -1
Вариант 19
11 6 -18
-8 -4 14
4 3 -5
Вариант 20
3 1 1
-2 -3 -2
0 3 2
| Вариант 21
0 -1 -1
5 6 7
-3 -3 -4
Вариант 22
-8 -18 -10
2 5 2
3 6 5
Вариант 23
-8 -9 -10
4 5 4
3 3 5
Вариант 24
5 6 3
-6 -7 -3
4 6 4
Вариант 25
5 -6 -6
6 -7 -6
-2 3 4
Вариант 26
5 3 3
-12 -9 -10
6 5 6
Вариант 27
1 -4 2
1 3 1
-1 2 -2
Вариант 28
2 -3 0
2 -11 2
9 -57 11
Вариант 29
21 7 20
-36 -10 -36
-10 -4 -9
Вариант 30
-2 -1 1
-9 2 3
-3 -3 2
|
| Вариант 31
3 -4 4
-1 0 2
-3 3 -1
Вариант 32
-5 -2 6
-6 -1 6
-7 -2 8
Вариант 33
4 -6 2
9 -19 6
24 -54 17
Вариант 34
1 -4 -2
-2 -9 -4
4 22 10
Вариант 35
-1 -14 -8
1 8 4
-2 -10 -4
Вариант 36
-5 -13 -11
4 10 8
-2 -4 -2
Вариант 37
-2 -2 -2
5 5 4
-1 -1 0
Вариант 38
2 4 0
-1 -2 -1
1 2 3
Вариант 39
-2 2 6
3 -1 -6
-2 2 6
Вариант 40
-2 -2 -12
-3 -1 -12
1 1 6
| Вариант 41
-5 -8 -6
2 4 2
3 4 4
Вариант 42
-3 24 -5
-1 6 -1
-2 6 0
Вариант 43
9 -2 -3
-3 2 1
24 -6 -8
Вариант 44
-1 2 -2
-7 8 -6
-6 6 -4
Вариант 45
0 -8 -4
1 5 2
-2 -6 -2
Вариант 46
-1 18 16
1 -8 -8
0 12 10
Вариант 47
7 21 27
-4 -14 -20
2 6 8
Вариант 48
-6 -4 -4
-1 0 -1
9 6 7
Вариант 49
6 4 4
-11 -9 -10
3 3 4
Вариант 50
2 0 4
1 4 1
-3 -6 -5
| Вариант 51
2 0 4
2 4 2
-3 -3 -5
Вариант 52
4 -6 -12
-3 7 12
2 -6 -10
Вариант 53
4 6 24
3 7 24
-1 -3 -10
Вариант 54
-5 -3 -3
12 6 4
-6 -2 0
Вариант 55
11 16 10
-4 -6 -4
-5 -8 -4
Вариант 56
7 -42 9
1 -4 1
0 12 -2
Вариант 57
-13 4 5
9 -2 -3
-42 12 16
Вариант 58
8 -1 -6
6 1 -6
10 -1 -8
Вариант 59
-10 24 -8
-9 19 -6
-15 27 -8
Вариант 60
2 16 8
-1 -3 -2
2 2 2
|
| Вариант 61
2 -18 -16
-1 9 8
0 -12 -9
Вариант 62
-6 -21 -27
4 15 20
-2 -6 -7
Вариант 63
7 4 4
1 1 1
-9 -6 -6
Вариант 64
-5 -4 -4
11 10 10
-3 -3 -3
Вариант 65
-1 0 -4
-1 -3 -1
3 6 6
Вариант 66
-1 0 -4
-2 -3 -2
3 3 6
Вариант 67
6 3 3
-12 -5 -4
6 2 1
Вариант 68
-10 -16 -10
4 7 4
5 8 5
Вариант 69
-6 42 -9
-1 5 -1
0 -12 3
Вариант 70
14 -4 -5
-9 3 3
42 -12 -15
| Вариант 71
-2 2 -2
-13 13 -10
-12 12 -9
Вариант 72
-7 1 6
-6 0 6
-10 1 9
Вариант 73
11 -24 8
9 -18 6
15 -27 9
Вариант 74
-1 -16 -8
1 4 2
-2 -2 -1
Вариант 75
-3 20 20
2 -9 -10
-1 13 12
Вариант 76
7 25 35
-4 -17 -26
2 7 10
Вариант 77
-8 -5 -5
-1 0 -1
11 7 8
Вариант 78
7 5 5
-14 -12 -13
4 4 5
Вариант 79
3 2 6
1 4 1
-4 -8 -7
Вариант 80
3 1 6
2 4 2
-4 -4 -7
| Вариант 81
4 -8 -15
-3 9 15
2 -8 -13
Вариант 82
4 8 30
3 9 30
-1 -4 -13
Вариант 83
-7 -4 -4
16 8 6
-8 -3 -1
Вариант 84
13 20 12
-5 -8 -5
-6 -10 -5
Вариант 85
10 -1 -8
8 1 -8
13 -1 -11
Вариант 86
-13 30 -10
-12 25 -8
-21 39 -12
Вариант 87
2 20 10
-1 -3 -2
2 0 1
Вариант 88
8 5 5
3 4 3
-13 -11 -10
Вариант 89
-7 -5 -5
12 10 9
-2 -2 -1
Вариант 90
5 14 2
-3 -8 -3
2 4 5
|
В задачах 91-180 есть кратный корень
| Вариант 91
3 -2 -4
-1 2 2
1 -1 -1
Вариант 92
0 -1 -1
3 4 3
-1 -1 0
Вариант 93
3 1 1
-4 -1 -2
2 1 2
Вариант 94
-1 -4 -2
1 3 1
1 2 2
Вариант 95
-3 -1 -4
-12 -2 -12
8 2 9
Вариант 96
4 -1 -1
-3 2 1
9 -3 -2
Вариант 97
1 0 0
-3 4 -2
-3 3 -1
Вариант 98
-1 0 2
-2 1 2
-3 0 4
Вариант 99
4 -6 2
3 -5 2
6 -12 5
Вариант 100
-2 -8 -4
1 4 1
1 2 3
| Вариант 101
-2 -4 -4
2 4 2
1 1 3
Вариант 102
3 1 1
-4 -2 -4
2 2 4
Вариант 103
3 -6 1
1 -4 1
4 -24 6
Вариант 104
14 4 12
-12 -2 -12
-9 -3 -7
Вариант 105
-1 0 1
-3 2 1
-6 0 4
Вариант 106
0 -1 2
-2 1 2
-2 -1 4
Вариант 107
2 0 0
-1 -3 -2
2 10 6
Вариант 108
7 -8 -16
-4 3 8
4 -4 -9
Вариант 109
7 4 4
0 -1 0
-8 -4 -5
Вариант 110
-5 -4 -4
12 11 12
-4 -4 -5
| Вариант 111
-5 -8 -8
0 -1 0
4 8 7
Вариант 112
-5 -4 -8
0 -1 0
4 4 7
Вариант 113
-1 8 12
0 -9 -12
0 8 11
Вариант 114
7 4 4
-16 -9 -8
8 4 3
Вариант 115
-9 -16 -8
4 7 4
4 8 3
Вариант 116
11 -4 -4
-12 3 4
36 -12 -13
Вариант 117
5 12 4
-2 -5 -2
3 9 4
Вариант 118
7 9 3
-4 -5 -2
2 3 2
Вариант 119
0 -1 -1
-1 0 -1
3 3 4
Вариант 120
3 1 1
-2 0 -1
0 0 1
|
| Вариант 121
5 4 4
-1 0 -1
-2 -2 -1
Вариант 122
4 -15 3
1 -4 1
3 -15 4
Вариант 123
-4 1 2
0 1 0
-15 3 7
Вариант 124
3 -2 2
4 -3 4
3 -3 4
Вариант 125
2 4 2
-1 -3 -2
2 8 5
Вариант 126
9 24 8
-4 -11 -4
6 18 7
Вариант 127
13 18 6
-8 -11 -4
4 6 3
Вариант 128
-1 -2 -2
-2 -1 -2
6 6 7
Вариант 129
9 8 8
-2 -1 -2
-4 -4 -3
Вариант 130
7 -30 6
2 -9 2
6 -30 7
| Вариант 131
-9 2 4
0 1 0
-30 6 13
Вариант 132
5 -4 4
8 -7 8
6 -6 7
Вариант 133
3 8 4
-2 -7 -4
4 16 9
Вариант 134
-16 -15 15
12 11 -12
-6 -6 5
Вариант 135
11 24 12
-3 -7 -3
-3 -6 -4
Вариант 136
11 12 12
-6 -7 -6
-3 -3 -4
Вариант 137
-4 -3 -3
12 11 12
-6 -6 -7
Вариант 138
-4 18 -3
-3 17 -3
-12 72 -13
Вариант 139
5 3 -6
6 2 -6
6 3 -7
Вариант 140
-4 -5 5
4 5 -4
-2 -2 3
| Вариант 141
1 0 0
-1 0 -2
1 1 3
Вариант 142
5 8 4
-1 -1 -1
-1 -2 0
Вариант 143
5 4 4
-2 -1 -2
-1 -1 0
Вариант 144
0 -1 -1
4 5 4
-2 -2 -1
Вариант 145
0 6 -1
-1 7 -1
-4 24 -3
Вариант 146
-11 -4 -12
12 5 12
9 3 10
Вариант 147
3 1 -2
2 2 -2
2 1 -1
Вариант 148
-2 4 8
2 -0 -4
-2 2 6
Вариант 149
4 2 2
-6 -4 -6
2 2 4
Вариант 150
-2 -2 -2
8 6 4
-4 -2 0
|
Литература
1. Горбанёв Н.Н., Ельцов А.А., Магазинников Л.И. Линейная алгебра. Аналитическая геометрия. Томск, 2001. 164 с.
2. Курош А.Г. Курс высшей алгебры. – Москва Физматгиз, 1963 – 432 с.
3. Магазинников Л.И., Магазинникова А.Л. Практикум по линейной алгебре и аналитической геометрии. Томск, 2005. 104 с.
4. Александрова Н.В. Из истории векторного исчисления. Москва, Изд-во МАИ, 1992. 152 с.

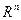 называется отображение
называется отображение  , сопоставляющее каждой паре векторов число, причём:
, сопоставляющее каждой паре векторов число, причём: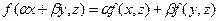
 .
.
 .
. .
. для билинейной формы, то полученное отображение
для билинейной формы, то полученное отображение  называется квадратичной формой на пространстве
называется квадратичной формой на пространстве  . Поскольку
. Поскольку  , то на значение квадратичной формы влияют только суммы вида
, то на значение квадратичной формы влияют только суммы вида  , а не каждое слагаемое в отдельности. Отсюда очевидно, что квадратичную форму всегда можно задать с помощью симметрической матрицы.
, а не каждое слагаемое в отдельности. Отсюда очевидно, что квадратичную форму всегда можно задать с помощью симметрической матрицы. , то она называется квадратичной формой в каноническом виде.
, то она называется квадратичной формой в каноническом виде. .
.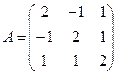
 . Простому корню 0 соответствует собственный вектор
. Простому корню 0 соответствует собственный вектор 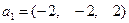 , кратному корню 3 соответствуют два собственных вектора:
, кратному корню 3 соответствуют два собственных вектора: 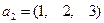 ,
,  . Запишем матрицу перехода, предварительно поделив каждый вектор на его модуль.
. Запишем матрицу перехода, предварительно поделив каждый вектор на его модуль. ,
,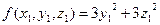 .
.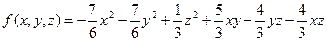

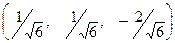
 .
.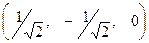
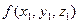 =
=  .
.


