Управления и радиоэлектроники
http://blog.shikate.ru/category/shikate/bibliotechnyj-yumor/
Томский государственный университет систем
Кафедра высшей математики (ВМ) Приходовский М.А. ЛИНЕЙНЫЕ ОПЕРАТОРЫ И КВАДРАТИЧНЫЕ ФОРМЫ Практическое пособие и комплект задач
Содержание §1. Определение линейного оператора. Матрица линейного оператора. 1.2 Графическое представление линейного оператора. §2. Построение матрицы линейного оператора. 2.1 Построение матрицы по заданной формуле отображения. 2.2 Построение матрицы по отображаемым системам векторов. 2.3 Прочие способы нахождения матрицы оператора. 2.4 Сумма, произведение линейных операторов. §3. Нахождение собственных чисел и собственных векторов. 3.1 Все характеристические корни действительны и различны. 3.2 Среди характеристических корней есть кратные. 3.3 Не все характеристические корни действительны. 3.3 Собственные подпространства. 3.5 Матрица линейного оператора в новом базисе. 3.6 Построение матрицы оператора по известным собственным числам и векторам. §4. Симметрические операторы. Квадратичные формы. 4.1 Симметрические операторы и их свойства. 4.2 Билинейные и квадратичные формы. §5. Приложения. Задачи для самостоятельного решения.
Разработчик: доцент кафедры ВМ Приходовский Михаил Анатольевич Определение 1. Отображение L из линейного пространства 1) 2) Эти 2 равенства эквивалентны 3): 3) Заметим, что линейный оператор отображает нулевой вектор в нулевой вектор. По свойству линейности, Любая матрица размера
Таким образом, каждая квадратная матрица задаёт преобразование, или отображение, в пространстве размерности n. Отображения, вводимые таким образом, будут линейными, что следует из свойств умножения матриц:
Аналогично из свойства Если отобразить вектор
То есть образом будет вектор, координаты которого есть элементы первого столбца в матрице, задающей отображение. Аналогично, для вектора ei образ будет вектором, координаты которого – элементы столбца номер i рассматриваемой матрицы. Итак, матрица задаёт линейное отображение векторов. С другой стороны, любое линейное отображение L конечномерных пространств можно задать с помощью матрицы. Представим вектор x в виде откуда видно, что образ вектора зависит лишь от координат этого самого вектора и от того, куда отображаются оператором n базисных векторов пространства, то есть зависит от векторов Замечание. Для сравнения рассмотрим линейный оператор, отображающий векторы в пространстве
|

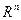 в линейное пространство
в линейное пространство 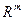 называется линейным отображением, или линейным оператором, если для любых векторов
называется линейным отображением, или линейным оператором, если для любых векторов  из
из 
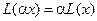

 .
. задаёт линейное отображение пространства
задаёт линейное отображение пространства 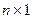 согласованы. В частности, квадратную матрицу порядка n можно умножать на вектор-столбец, состоящий из n координат, так как размеры матриц будут n´n и n´1, и результатом будет матрица-столбец размера n´1.
согласованы. В частности, квадратную матрицу порядка n можно умножать на вектор-столбец, состоящий из n координат, так как размеры матриц будут n´n и n´1, и результатом будет матрица-столбец размера n´1.
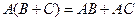 для любых матриц A,B,C, размеры которых согласованы и возможно их умножение, поэтому
для любых матриц A,B,C, размеры которых согласованы и возможно их умножение, поэтому 
 следует
следует 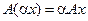 .
. то получим
то получим
 , где
, где  - координаты,
- координаты,  - базисные векторы, то по свойству линейности оператора получим
- базисные векторы, то по свойству линейности оператора получим 

 ,
, . Матрица, составленная из этих векторов (по столбцам), является матрицей линейного оператора.
. Матрица, составленная из этих векторов (по столбцам), является матрицей линейного оператора. . Этот оператор – знакомое ещё из школы линейное отображение вида
. Этот оператор – знакомое ещё из школы линейное отображение вида  . Причём коэффициент
. Причём коэффициент 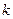 может рассматриваться в качестве матрицы оператора (матрица порядка 1), x – вектор в пространстве
может рассматриваться в качестве матрицы оператора (матрица порядка 1), x – вектор в пространстве  . Задать линейное отображение
. Задать линейное отображение  , и образа единицы:
, и образа единицы: 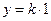 .
.


