Упражнения. 1.58. Определить угол раствора 2γ стрельчатой лапы, обеспечивающей резание со скольжением, если угол трения почвы о лезвие φn
1.58. Определить угол раствора 2γ; стрельчатой лапы, обеспечивающей резание со скольжением, если угол трения почвы о лезвие φn, а корней сорных растений φс.
1.59. Определить расстояние L между рядами рыхлительных лап культиватора, если глубина обработки h, вылет носка лапы l0, угол вхождения лапы в почву α;, угол внутреннего трения почвы φвн. Решение сопроводить расчетной схемой.
1.60. Определить расстояние B между соседними рыхлительными лапами в ряду, если ширина лапы b0, глубина обработки h, угол вхождения лапы в почву α;, угол
1.61. Подобрать рабочие органы и составить схему расстановки рыхлительных лап культиватора для сплошной обработки почвы при следующих условиях: глубина обработки h =0,15 м, угол δ;=25°…30°, ширина лапы b0 =50 мм, вылет носка лапы l0 =0,15 м, угол вхождения лапы в почву α;=40°.
1.62. Подобрать рабочие органы и составить схему расстановки полольных лап культиватора, если предусматривается междурядная обработка посевов с шириной междурядья 0,7 м и защитной зоной 0,15 м при наличии лап с шириной захвата 0,27 м; 0,22 м и 0,165 м.
1.63. Определить приращение тягового сопротивления стрельчатой лапы и суммарную величину усилия вдоль лезвия при подрезании единичного корня сорняка, если известны: 2γ;=65°, угол трения корня сорняка о лезвие φ;=42°, а нормальная реакция лезвия лапы N =1,5 Н. Решение сопроводить расчетной схемой.
1.64. Определить удельную работу резания почвы односторонней культиваторной лапой при угле раствора γ; и ширине захвата b, если угол трения почвы о сталь φ; и равнодействующая сил сопротивления резанию R.
4.1.9. Дисковые почвообрабатывающие орудия
Основными конструктивными параметрами сферических дисков, определяющими их воздействие на почву при той или иной установке к линии движения орудия, являются диаметр D диска и радиус кривизны R (рисунок 4.18), причем D=2R×sinφ;, (4.37) где φ; – половина угла при вершине сектора. Основными геометрическими характеристиками диска заданных размеров, определяющих его работоспособность на глубине а, при установке под углом
Рисунок 4.18 - Сферический диск
Рисунок 4.19 - Схема к определению геометрических характеристик сферического диска
где εа – затылочный угол; ωа – угол наклона образующей конуса заточки к плоскости режущей кромки (сечение 2-2). Хорда Dа (см. рисунок 4.19) погружения диска на глубину а определяется по выражению
Расстояние между смежными дисками лущильника определяется по формуле
где с – высота гребней дна борозды. Тяговое сопротивление одиночного сферического диска может быть определено по приближенной формуле
где k – коэффициент удельного сопротивления почвы, k =4…8 Н/см2.
Пример 41. Определить величину затылочного угла ε;a для диска лущильника диаметром D =450 мм, радиусом сферы R =600 мм, глубине хода а =0,10 м, угле атаке α;=35° и угле заострения i =15°. Решение: Из расчетных схем (см. рисунки 4.18 и 4.19) следует, что εа=α-ωа. (1) Известно [6], что
где Поэтому
Из рисунка 4.18 следует, что
где i – угол заострения. Численное значение угла φ; определяем по выражению (4.37)
Решая совместно (4), (5) и (3), получим
Подставив исходные данные в выражения (6), будем иметь
Отсюда искомое ε;a по выражению (1): εa=α-ωa =35°-32°=3°. Ответ: εa = 3°.
Пример 42. Определить максимальную глубину хода дисков лущильника с параметрами: D =450 мм, R =600 мм, α;=35° и i =15°. Решение: Предельная глубина хода диска, исходя из устойчивости его движения, будет при εa =0. Поэтому по выражению (6) (см. пример 41) будем иметь: α=ωа =35°; ω;=37°. Для решения задачи используем выражение (3) примера 41:
Возведя в квадрат это выражение, получим уравнение
Решение полученного уравнения дает:
Подставив значения D =450 мм, ωа=α;=35° и ω;=37°, получим
Или: а1 =296 мм; а2 =154 мм. Физический смысл имеет только корень уравнения а2 =154 мм. Поэтому аmax=а2 =154 мм. Ответ: аmax= 154 мм.
Пример 43. Определить расстояние b между смежными дисками лущильника с параметрами: D =450 мм; с =35 мм; α;=35°. Решение: По формуле (4.40) имеем:
Ответ: b = 166 мм.
Пример 44. Определить тяговое сопротивление одиночного сферического диска при следующих условиях: k =4 Н/см2; D =450 мм; α;=35°; а =120 мм. Решение: Используя приближенную формулу (4.41), будем иметь:
Ответ: Rx =97 Н.
|

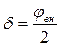 . Решение сопроводить расчетной схемой.
. Решение сопроводить расчетной схемой. (α; – угол атаки, т.е. угол между плоскостью вращения диска и направлением движения орудия) к линии m-m рабочего движения (рисунок 4.19), являются затылочный угол ε; и угол наклона ω; образующей конуса заточки к плоскости режущей кромки. Для любого сечения диска горизонтальной плоскостью имеем
(α; – угол атаки, т.е. угол между плоскостью вращения диска и направлением движения орудия) к линии m-m рабочего движения (рисунок 4.19), являются затылочный угол ε; и угол наклона ω; образующей конуса заточки к плоскости режущей кромки. Для любого сечения диска горизонтальной плоскостью имеем

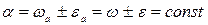 , (4.38)
, (4.38) . (4.39)
. (4.39) , (4.40)
, (4.40)
 (4.41)
(4.41) (2)
(2)
 . (3)
. (3) , (4)
, (4)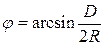 . (5)
. (5)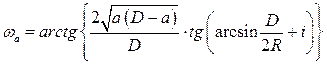 . (6)
. (6)
 .
. .
.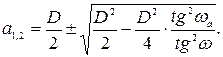

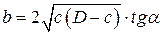 =
=  мм.
мм. Н.
Н.


