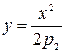Упражнения. 1.17. Определить горизонтальную составляющую тягового сопротивления двугранного клина от силы тяжести пласта
1.17. Определить горизонтальную составляющую тягового сопротивления двугранного клина от силы тяжести пласта. Объемная масса почвы γоб =1300 кг/м3, длина рабочей поверхности l, ширина захвата клина b, глубина хода клина а, рабочей угол клина α;. Силой трения о поверхности клина пренебречь.
1.18. Определить горизонтальную составляющую тягового сопротивления двугранного клина от силы тяжести пласта и сил трения, возникающих при скольжении пласта по рабочей поверхности клина. Известны: γоб =1300 кг/м3; l, b, a, α, φ;.
1.19. Определить горизонтальную составляющую тягового сопротивления двугранного клина от динамического давления пласта почвы, обусловленного силой инерции. Известны: γоб =1300 кг/м3; b, a, α, φ, υ;.
1.20. Определить горизонтальную составляющую силы сопротивления снятию почвы затупленным лезвием клина. Известны: b, q0, h, εз, φ;.
1.21. Определить общую величину тягового сопротивления двугранного клина по условиям упражнений 1.18, 1.19, 1.20 без учета силы сопротивления на деформацию почвы.
1.22. Определить наибольшую длину рабочей поверхности клина, если заданы: γоб =1300 кг/м3; b, a, α, υ;, σсж = 90 кПа.
1.23. Определить вертикальную составляющую силы сопротивления смятию почвы затупленным лезвием клина. Если известны b =0,7 м; q0 =10 Н/см3; высота затылочной фаски h =5 мм; угол трения почвы φ;=250; угол затылочной фаски ε;з=250.
1.24. Определить временное сопротивление почвы сжатию σсж двугранным клином, если известны: γоб =1300 кг/м3; b =0,7 м, а =0,25 м, α;=200; φ;=250; υ; =2,2 м/с; l =0,3 м. Указание: Использовать формулу (7) примера 15.
4.1.4. Проектирование рабочей поверхности корпуса плуга
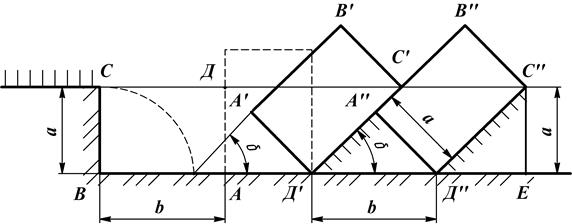
Допустим, что пласт и стенка борозды в процессе вспашки не изменяют свои размеры, т.е. пласт условно не деформируется [6]. Построение профиля борозды показано на рисунке 4.8.
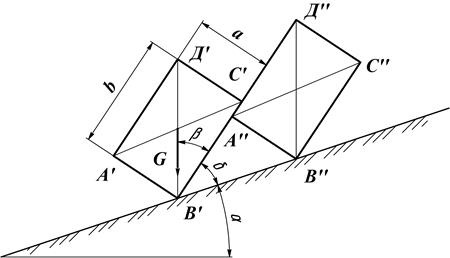
Рисунок 4.8 - Схема оборота пласта Пусть а – глубина пахоты, b – ширина захвата корпуса плуга, k=b/a, δ; – угол наклона отваленного пласта к горизонту. Минимальный радиус направляющей кривой Rmin определяется из условия, когда пласт, поднимаемый отвалом, целиком помещается на нем, не пересыпаясь через отвал
где b – ширина захвата корпуса плуга, ε;0 – угол постановки лемеха ко дну борозды, γ0 – угол постановки лезвия лемеха к стенке борозды. Максимальный радиус кривизны направляющей кривой определяется из условия, что бороздной обрез отвала не задирает отваленного пласта
где k=b/a; θ – угол между горизонтальной плоскостью и касательной плоскостью к отвалу, определяемый по формуле Характер изменения угла γ=f(z) в интервале z1…zmax: для отвалов культурного типа
для отвалов полувинтового типа
где у, х и р – параметры, определяемые по расчетам (см. пример).
Пример 16. Определить предельную глубину a вспашки плугом, если ширина захвата корпуса плуга b. Решение: Для того, чтобы после прохода корпуса плуга пласт не опрокидывался обратно в открытую борозду, центр тяжести площади поперечного сечения пласта должен лежать правее точки опоры В' пласта о дно борозды. Положение диагонали Д'В', при котором пласт еще может сохранить свое положение, хотя и неустойчивое (рисунок 4.9), будет предельным. Из подобия прямоугольных треугольников
или
Рисунок 4.9 - К обоснованию максимальной глубины вспашки
Возведя в квадрат, правые и левые части (1), получим а4+а2b2=b4 (2) Разделив уравнение (2) на а4 и имея ввиду k=b/a, получим биквадратное уравнение k4-k2-1=0. (3) Решая это биквадратное уравнение (3), имеем kmin= 1,27. (4) Следует заметить, что в реальных условиях оборот пласта плугом без предплужника получается при k =1,5, на рыхлых почвах k =1,3, а на старопахотных почвах k =1,5…1,75. Поэтому теоретическая максимальная глубина amax вспашки плугом при заданной ширине захвата корпуса определится
Ответ:
Пример 17. Определить предельную глубину вспышки плугом ПЛН-4-35 с предплужником. Решение: Предельная глубина вспышки плугом с предплужником определяется из выражения
где kmin пр – соотношение находится аналогично рассмотренному примеру 16: kmin пр = 0,94; для старопахотных почв при работе с предплужником рекмоендуется принимать kпр = 1,14…1,25. Поскольку ширина захвата корпуса плуга ПЛН-4-35 b =0,35 м, то предельная теоретическая глубина вспышки
Предельная глубина вспышки старопахотных почв при работе с предплужником будет варьировать в пределах:
Ответ: аmax =0,372 м.
Пример 18. Имеются два плужных корпуса. Основные параметры первого плужного корпуса γ0 =42°, γmax= 48°; второго: γ0 =38°, γmax =50°. К какому типу относится первая и вторая рабочие поверхности плужных корпусов? Решение: Рабочие поверхности плужных корпусов отличаются по значению ∆γ=γmax-γ0. Поэтому: 1) ∆γ = 48°-42°=6° – культурная рабочая поверхность 2) ∆γ; = 50°-38°=12° – полувинтовая рабочая поверхность. Ответ: первый плужный корпус – культурная рабочая поверхность, второй плужный корпус – полувинтовая рабочая поверхность.
Пример 19. Определить предельную величину отношения ширины пласта к глубине вспышки Решение: Приведем расчетную схему (рисунок 4.10) Из приведенной схемы следует, что критическим условием устойчивости является
В выражении (1) неизвестными являются δ; и β;, которые могут быть определены из прямоугольных треугольников B ' A '' B '' и B ' D ' C ':
Отсюда, имея в виду, что
Рисунок 4.10 - Схема к определению α = f(k)
Подставив выражение (2) и (3) в (1), получим
Подставив в (4) значения k в интервале от 1 до 3, получим численные значения α для построения графика α = f(k).
Таблица 4.1 - Таблица расчетных данных
На рисунке 4.11 приведен график зависимости α = f(k).
Рисунок 4.11 - График зависимости α = f(k)
Из полученной графической зависимости следует, что на склоновых землях для проведения отвальной вспашки необходимо увеличивать соотношение
Пример 20. Определить радиусы Rmin и Rmax направляющей кривой культурного отвала при следующих исходных данных: ширина захвата корпуса плуга b =0,35 м, глубина пахоты а =0,27 м, угол ε0 =27°, угол γ0 =42°. Решение: Наименьшее значение радиуса определим по формуле (4.14)
Максимальное значение радиуса направляющей кривой определим по формуле (4.15)
Значение угла θ находим по равенству
Ответ: Rmin =0,425 м, Rmax =0,76 м.
Пример 21. Произвести расчет и построить график для образующих культурного отвала с параметрами: γ0 =390; γmin =37,50; γmax =460. Решение: Характер изменения
Рисунок 4.12 - Характер изменения
От опорной плоскости лезвия лемеха до высоты z1 (z1 = 50…100 мм) наклон образующей к стенке борозды уменьшается до γmin. Это делается для того, чтобы облегчить подъем пласта на грудь отвала и сдвиг его в борозду. Принимаем z1 =75 мм. От z =0 до z1 =75 мм располагаем образующие с интервалом 25 мм. При линейной зависимости ∆γ; от x разность значений двух соседних образующих равна Следовательно, промежуточные значения γ; будут равны 38030′ и 380. В интервале от z1 до zmax образующие располагаем через 50 мм. Вычисляем значения x для всех промежуточных образующих: результаты сводим в таблицу 4.2. По формуле (4.16)
вычисляем промежуточные значения у и результаты также заносим в эту таблицу. Для определения размерного коэффициента λ; находим:
Когда определены коэффициент λ; и значение у, находим ∆γ; для каждой из образующих, пользуясь выражением ∆γ=λγ;. Приращения ∆γ; получаются в долях градусов, например ∆γ; = λγ;=1,960; переводим в градусы и минуты, получаем ∆γ; =1058′. Когда найдены ∆γ;, вычисляем угол для каждой образующей: γ=γmin+∆γ;.
Таблица 4.2 - Расчетные данные для интервала от z1 до zmax
После завершения расчетов на миллиметровой бумаге следует построить график γ=f(z).
Пример 22. Произвести расчет и построить график для образующих полувинтового отвала с параметрами: γ0 =370; γmin =350; γmax =450. Решение: Для рабочей поверхности полувинтового типа (рисунок 4.13) при расчете промежуточных значений угла γ; необходимо определять параметры р1 и р2. Поскольку согласно (4.17)
то параметр р1 – для левой ветви, параметр р2 – для правой.
Рисунок 4.13 - Характер изменения
Так как в этом случае мы имеем два неизвестных р и λ;, то принимаем В интервале от γ0 до γmin имеем:
Отсюда
В интервале от γmin до γmax имеем:
Отсюда Последующие расчеты промежуточных значений γ; сведены в таблицы 4.3 и 4.4. В тех же осях координат (см. пример 21) построить зависимость
Таблица 4.3 - Расчетные данные для интервала от z =0 до z=z1
Таблица 4.4 - Расчетные данные для интервала от z1 до zmax
|

 (4.14)
(4.14)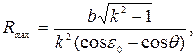 (4.15)
(4.15) .
.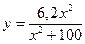 , (4.16)
, (4.16)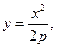 (4.17)
(4.17) ,
,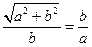 . (1)
. (1)
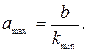 (5)
(5) , (1)
, (1)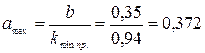 м.
м.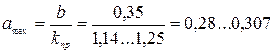 м.
м.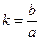 и построить график изменения величины α = f(k) при условии, если пахота будет производиться поперек склона с углом α; на подъем.
и построить график изменения величины α = f(k) при условии, если пахота будет производиться поперек склона с углом α; на подъем. . (1)
. (1)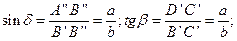
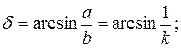 (2)
(2) (3)
(3)
 (4)
(4)
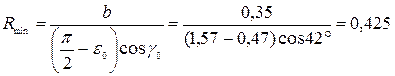 м.
м.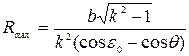 .
.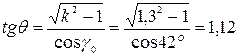 или θ;=48010′;
или θ;=48010′; м.
м. для образующих культурного отвала выражается следующим графиком (рисунок 4.12).
для образующих культурного отвала выражается следующим графиком (рисунок 4.12).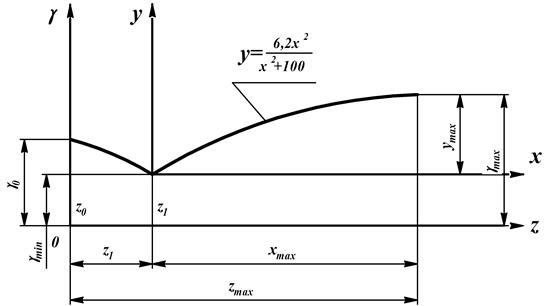


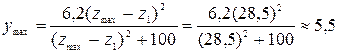 см.
см. .
.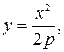

 и, исходя из граничных значений угла, определяем р1 и р2.
и, исходя из граничных значений угла, определяем р1 и р2.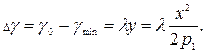
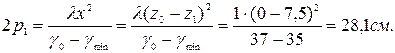
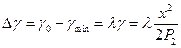 .
. см.
см.