ЗАДАЧИ И УПРАЖНЕНИЯ
4.1. МАШИНЫ И ОРУДИЯ ДЛЯ ОБРАБОТКИ ПОЧВЫ
4.1.1. Деформации почвы, возникающие при работе двугранного клина
Деформация почв под воздействием клина зависит от величины угла крошения α; и свойств почвы. При обработке супесчаных почв, обладающих малой связностью, деформация почвы складывается из двух периодически повторяющихся фаз [8]: уплотнения клином почвы и вдавливания ее частиц в еще не деформированную массу при перемещении клина из точки О в точку О1 и мгновенного возникновения в почве впереди клина плоскости сдвига, образующей угол ψ; с дном борозды (рисунок 4.1 а). При этом происходит отделение от массива почвы призмовидной части пласта, имеющей в поперечном сечении форму трапеции О1А1АВ. Не претерпевая новых деформаций, эта часть начинает двигаться по поверхности клина со скоростью υr и одновременно скользить по плоскости сдвига О1А1 со скоростью υа. Из треугольника скоростей (рисунок 4.1 а) находим:
где υ; - скорость поступательного движения клина, м/с; α; - угол клина, град; ψ; - угол между плоскостью сдвига пласта и дном борозды, град. Деформация супесчаной почвы путем сдвига сопровождается с «усадкой» пласта, то есть увеличением его толщины а1
Угол ψ; может быть определен из выражения [7]:
где φ; - угол трения материала рабочей поверхности клинка о почву, град; φвн - угол внутреннего трения почвы, град. При обработке влажной задернелой суглинистой почвы клином с малым углом крошения α; пласт имеет вид сплошной ленты [8]. В действительности сплошность такого пласта нарушена трещинами, возникающими при изгибе пласта в начальный момент его поступления на рабочую поверхность клина.При движении пласта по плоскости клина трещины смыкаются и пласт приобретает вид сплошной ленты (рисунок 4.1 б). Толщина пласта а1 равна глубине хода клина а,
Рисунок 4.1 - Деформация почвы под воздействием клина: а – деформация супесчаной почвы; б – деформация суглинистой почвы; в – упрощенная схема деформации
поэтому усадки пласта не происходит и относительная скорость движения пласта υr равна скорости поступательного движения клина υ;. Из треугольника скоростей находим скорость абсолютного движения частиц пласта υа =2 u sin Для решения ряда практических задач, например размещения рабочих органов на раме машины, принимают упрощенную схему деформации почвы клином (рисунок 4.1 в). Предполагают [6], что на основании теории наибольших касательных напряжений разрушение пласта происходит вблизи действия силы R по некоторой ломанной К, расположенной между сечениями Н1 и Н2 под углом внутреннего трения почвы φвн симметрично к силе R. Поэтому усилие R, с которым плоский клин действует на пласт, отклоняется от нормали N на угол трения φ;
Пример 1. Супесчаная почва деформируется двугранным клином с углом крошения α = 20°. Коэффициент трения почвы о рабочую поверхность клина f = 0,29, а коэффициент внутреннего трения почвы fвн =1,04. Определить скорости абсолютного и относительного движения пласта, если скорость поступательного движения клина υ = 1,5 м/с. Решение: Поскольку f=tgφ; и fвн=tgφвн, то φ;=16,17º и φвн =46,17°. Численное значение угла ψ; можно определить по выражению (4.4)
Тогда скорости абсолютного и относительного движения частиц пласта можно вычислить по формулам (4.1) и (4.2)
Ответ: υа =0,55 м/с, υr =1,21 м/с.
Пример 2. Определить величину усадки пласта двугранным клином с углом крошения α;=25º при деформации им супесчаной почвы. Глубина хода клина а =0,2м, а значение угла ψ;=50°. Решение: Деформация супесчаных почв, обладающих малой связностью, сопровождается усадкой пласта (см.рисунок 4.1 а). Поэтому численное значение усадки пласта
где Следовательно:
Ответ: Δа ≈ 0,052 м.
Пример 3. Определить, на какую величину увеличится плотность ρ1 супесчаной почвы после деформации её двугранным клином, если глубина обработки а, высота (см. рисунок 4.1 а) положения максимально сжимаемой частицы почвы h. Решение: Пусть ширина захвата двугранного клина равна b. Тогда масса почвы в сечении ОАА1О1 (см. рисунок 4.1 а) определится выражением mп =ρ×a×s×b, (1) где ρ; – плотность почвы до её деформации, кг/м3; а – глубина хода клина, м; s – ширина сжимаемого элемента пласта, м. Под воздействием клина пласт почвы подвергается уплотнению, т.е. почва из объема, сечение которого ОВО1, сжимается и вдавливается в объем, сечение которого ВАА1О1. Поэтому
где ρ1 – плотность почвы после ее деформации, кг/м3; h – высота положения максимально сжимаемой частицы почвы, м. Из уравнений (1) и (2) следует:
Отсюда
Из уравнения (4) видно, что чем больше подвергается сжатию почва, то есть чем больше величина h, тем большим будет ее плотность. Однако при этом необходимо учитывать, что плотность деформируемой почвы не будет одинаковой по всему сечению пласта. Ответ:
Пример 4. Определить скорость абсолютного движения пласта при деформации влажной задернелой суглинистой почвы двугранным клином с углом крошения α;=20°, если скорость поступательного движения клина υ; =1,2 м/с. Решение: Поскольку при деформации влажной задернелой суглинистой почвы усадки пласта не происходит и относительная скорость движения пласта υr равна скорости поступательного движения клина υ;, то скорость υа абсолютного движения частиц пласта может быть определена по выражению (4.5.). υа = 2 u sin Ответ: υа =0,42 м/с.
Пример 5. Используя упрощенную схему (см. рисунок 4.1 в) деформации почвы двугранным клинком с углом α;, определить угол ψ; между плоскостью сдвига пласта и дном борозды. Решение: Пусть разрушение пласта происходит по некоторой ломанной К (см. рисунок 4.1 в) вблизи действия силы R. Требуется определить Поскольку острый угол между лучом АС и поверхностью клина ОА (
где φ; – угол трения материала рабочей поверхности клина о почву, град. Ответ: ψ=
|

 , (4.1)
, (4.1) , (4.2)
, (4.2)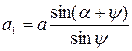 . (4.3)
. (4.3) , (4.4)
, (4.4)
 . (4.5)
. (4.5) . (4.6)
. (4.6)

 .
.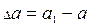 ,
, .
.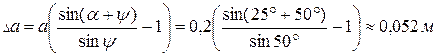 .
. , (2)
, (2) . (3)
. (3) . (4)
. (4) =0,42 м/с.
=0,42 м/с. RAC=ψ;.
RAC=ψ;. ,
, .
.


