Упражнения. 1.1. Супесчаная почва деформируется двугранным клином с углом крошения α
1.1. Супесчаная почва деформируется двугранным клином с углом крошения α;. Коэффициент трения почвы о рабочую поверхность клина f, а коэффициент внутреннего трения почвы fвн. Определить скорости абсолютного и относительного движения частиц пласта, если скорость поступательного движения клина υ;.
1.2. Определить величину угла α; двугранного клина, если им обрабатывается супесчаная почва, угол между плоскостью сдвига пласта и дном борозды ψ;, а соотношение скоростей равно υа / υ; r.
1.3. Определить величину угла ψ; между плоскостью сдвига пласта и дном борозды, если угол крошения α=0,5·φвн, а угол трения почвы о рабочую поверхность клина φ=0,3φвн. Величину φвн принять равной 45°.
1.4. Доказать, что a1=а
1.5. Определить величину усадки пласта двугранным клином с углом крошения α; при деформации им супесчаной почвы. Глубина хода клина а, а значение угла между плоскостью сдвига пласта и дном борозды ψ;.
1.6. Определить величину скорости абсолютного движения пласта при деформации влажной задернелой суглинистой почвы двугранным клином с углом крошения α;, если скорость поступательного движения клина υ;.
1.7. Определить величину угла α; двугранного клина, если им обрабатывается влажная задернелая суглинистая почва. Соотношение скоростей υа / υ;известно: 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 1,0.
1.8. Используя упрощенную схему (см. рисунок 4.1 в) деформации почвы двугранным клином с углом α;, определить угол ψ; между плоскостью сдвига пласта и дном борозды. Угол φ; трения материала рабочей поверхности клина о почву известен.
4.1.2. Деформации почвы, возникающие при работе трехгранного клина
Деформации почвы, возникающие под воздействием трехгранного клина, тождественны деформациям, возникающим при работе двугранного, т.е. деформация почвы сохраняется неизменной как при движении клина перпендикулярно лезвию (лобовое резание),так и при движении под углом γ; (косое резание) [8].Такой эффект воздействия на почву трехгранного клина становится понятным, если движение клина представить состоящим из чередующихся элементарных перемещений: перпендикулярно лезвию АВ и вдоль лезвия АВ (рисунок 4.2). Опытами, проведенными в лабораторных условиях[1,5,8], установлено, что при воздействии трехгранного клина на связную почву деформация происходит в результате отрыва, а при воздействии на песчаную (малосвязную) – в результате сдвига. Поэтому при определении траектории и скорости движения пласта примем, что его длина при подрезании и перемещении по клину не претерпевает изменения и, следовательно, скорость переносного движения пласта υ; равна скорости его относительного движения по поверхности клина υr. При подъеме на поверхность клина основание пласта, занимавшее положение АОС (см. рисунок 4.2), переходит в положение АО'С. Причем траекторией относительного движения является прямая АО', а абсолютной - ОО'. Полагая в треугольнике ОО'А сторону ОА равной переносной скорости υ;, а сторону АО' равной относительной скорости υr, принимаем, что υа ≡ Тогда
где l = СД – длина рабочей поверхности клина.
Рисунок 4.2 - Схема к определению траектории движения пласта
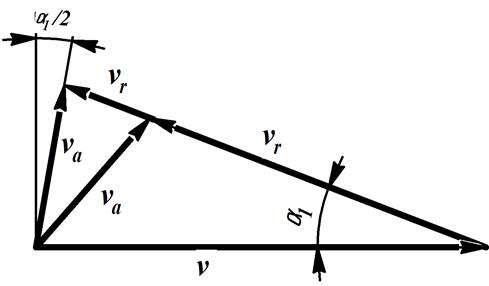
Рисунок 4.3 - К определению относительной и абсолютной скоростей движения пласта по рабочей поверхности клина (по плоскорежущей лапе) с усадкой
Исключив l из выражений (4.7), найдем
Установка стабилизаторов – рыхлителей на рабочей поверхности клина (например, на плоскорежущей лапе) приводит к изменению траекторий АО' и ОО' [4]. Пласт из положения АОС при подъеме на лапу переходит в положение АО''С', т.е. поднявшись в положение АО'С в плоскости АВД, совершает поворот на угол САС', равный разности углов ДАС и ОАС. Поэтому отрезок СО равен отрезку С'О'', отрезок АО равен отрезку АО'' и угол ОАС равен углу О''АС'=γ;. Поэтому
траекторией относительного движения является прямая АО'', а абсолютной - ОО''. Следовательно:
В ряде случаев, при работе почвообрабатывающих и землеройных пассивных рабочих органов в почвенном массиве возникает зона сжимающих напряжений, приводящих к необратимым деформациям (за пределы пропорциональности между напряжением и деформацией). Тогда скорость движения пласта по рабочей поверхности клина (например: по плоскорежущей лапе)
где Из векторного треугольника (рисунок 4.3.) можно определить:
Анализ полученных выражений (4.10) и (4.11.) показывает, что при i =0 величина υr =0, а
Пример 6. Определить величину скорости абсолютного движения пласта при деформации задернелой суглинистой почвы трехгранным клином с углами ε;=20° и γ;=35°, если скорость поступательного движения клина υ; =1,2 м/с. Решение: Поскольку при деформации влажной задернелой суглинистой почвы трехгранным клином усадки пласта не происходит и относительная скорость υr равна скорости поступательного движения клина υ; (по оси ОХ, см. рисунок 4.2), то абсолютная скорость движения частиц пласта υ; а может быть определено по выражению (4.8):
Ответ: υа =0,24 м/с.
Пример 7. Определить величину скорости абсолютного движения пласта при деформации задернелой суглинистой почвы трехгранным клином со стабилизаторами-рыхлителями, если скорость поступательного движения клина υ; =1,0 м/с, а угол α1= 18°. Решение: При установке стабилизаторов-рыхлителей на трехгранном клине траекторией относительного движения является прямая АО'', а абсолютной - ОО'' (см. рисунок 4.2). Поэтому по формуле (4.9) определим абсолютную скорость движения частиц пласта
Ответ: υа =0,31 м/с.
Пример 8. Определить величину скорости абсолютного движения пласта при деформации задернелой суглинистой почвы трехгранным клином со стабилизаторами-рыхлителями, если скорость поступательного движения клина υ; =1,0м/с, а угол α1 =18° и коэффициент усадки пласта i =0,6. Решение: Поскольку из векторного треугольника (см. рисунок 4.3) следует, что
то Ответ: υа =0,47м/с.
Пример 9. Определить величину коэффициента усадки пласта, если соотношение υа: υ; =0,5, а угол α1 =20°. Решение: Из выражения (4.11) с учетом υа / υ; =0,5 можно записать:
Решение полученного уравнения
При α1 =20° и υа / υ; =0,5 получим
i1 =0,57; i2 =1,31; поскольку 0<i<1, то коэффициент усадки пласта i =0,57. Ответ: i =0,57.
|

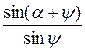 .
. .
.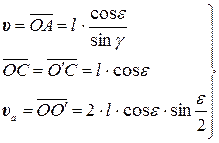 , (4.7)
, (4.7)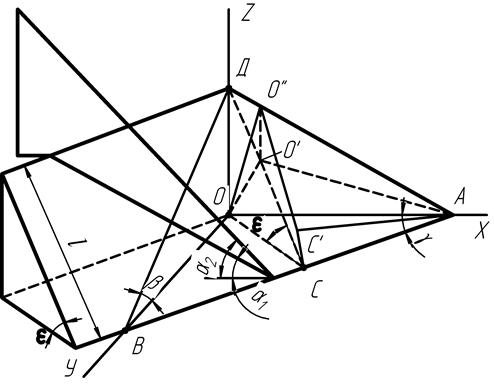
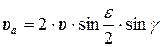 . (4.8)
. (4.8)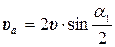 . (4.9)
. (4.9)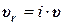 , (4.10)
, (4.10)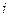 - коэффициент усадки пласта.
- коэффициент усадки пласта.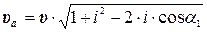 . (4.11)
. (4.11)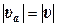 . Это свидетельствует, что при i =0 происходит сгруживание почвы. При i =1 величина
. Это свидетельствует, что при i =0 происходит сгруживание почвы. При i =1 величина  , а
, а 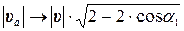 .
.
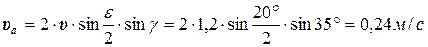
 .
.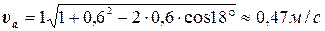 .
.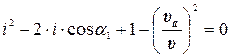 .
.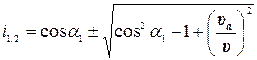 .
. ,
,


