Упражнения. 1.9. Определить величину скорости абсолютного движения пласта при деформации задернелой суглинистой почвы трехгранным клином с углами ε и γ (см
1.9. Определить величину скорости абсолютного движения пласта при деформации задернелой суглинистой почвы трехгранным клином с углами ε; и γ; (см. рисунок 4.2). Скорость поступательного движения клина υ;.
1.10. Определить величину скорости абсолютного движения пласта при деформации задернелой суглинистой почвы трехгранным клином со стабилизаторами-рыхлителями. Скорость поступательного движения клина υ;, а угол α1 (см. рисунок 4.2).
1.11. Определить величину скорости абсолютного движения пласта при деформации задернелой суглинистой почвы трехгранным клином со стабилизаторами-рыхлителями, если скорость поступательного движения клина υ;, угол α1 и коэффициент усадки пласта i (см. рисунок 4.2 и 4.3)
1.12.Определить величину коэффициента усадки пласта i, если известны соотношение υа: υ; и угол α1.
1.13. Определить величину угла α1 трехгранного клина, если им обрабатывается суглинистая почва, а соотношение скоростей равно υа / υ;.
По полученным данным построить график функции α1=f 1.14. Используя выражения (4.9.), доказать, что υа = υ;.
1.15. Используя выражения (4.11.), доказать, что υа = υ;.
1.16. Определить, при каком значении коэффициента усадки i соотношение скоростей υа / υ; =0,5. Величину угла α1 принят равным 20° (для решения задачи использовать выражение (4.11)).
4.1.3. Сопротивления почвы, возникающие при работе двугранного клина
При движении клина в почве возникают: сопротивление почвы проникновению в нее лезвия клина Rл, сопротивление почвы деформации, производимой рабочей поверхностью клина Rg, сила тяжести пласта G, инерция пласта F и силы трения, возникающие на рабочей поверхности клина, Т. По данным [8] сопротивление внедрению острого лезвия при работе клина в почве, не содержащей камней и прочных корней, можно учитывать вместе с сопротивлением почвы деформации, поскольку ни расчетным, ни экспериментальным путем этот вид сопротивления отдельно определить нельзя. При износе лезвия и образования у него затылочной фаски, производящей уплотнение слоя почвы на дне борозды, необходимо учитывать и этот вид сопротивления (рисунок 4.4). Затылочная фаска АВ лезвия уплотняет слой почвы высотой h на дне борозды, в результате чего возникает реактивная сила R3. Если принять, что сопротивление почвы смятию пропорционально величине деформации и пренебречь скруглением лезвия, то эпюра нормальных давлений почвы на затылочную фаску лезвия будет иметь форму треугольника. Максимальное значение давления почвы в точке В р =h×; q o, где qo – коэффициент объемного смятия почвы. Поскольку равнодействующая N3 элементарных нормальных сил сопротивления отклоняется на угол трения φ;, то
Рисунок 4.4 - Схема к определению силы сопротивления почвы при износе лезвия
где b -ширина захвата клина, м. Общая величина тягового сопротивления двугранного клина равна
где Rзx – горизонтальная составляющая силы сопротивления почвы при взаимодействии с затупленным лезвием (затылочной фаской), Н; Rgx – горизонтальная составляющая силы сопротивления почвы деформации, определяемая опытным путем, Н; RFX – горизонтальная составляющая силы сопротивления, необходимая для преодоления динамического давления пласта и обусловленная силой инерции, Н; RGX – горизонтальная составляющая силы сопротивления, необходимая для преодоления статистического давления пласта и обусловленная силой тяжести пласта, Н.
Пример 10. Определить горизонтальную составляющую тягового сопротивления двугранного клина от силы тяжести пласта. Объемная масса почвы Решение: Приведем расчетную схему (рисунок 4.5) На пласт действуют: реакция недеформированной почвы, находящейся впереди клина, QG; сила тяжести пласта G и результирующая элементарных нормальных сил сопротивления почвы RG на поверхности клина. Допустим, что пласт почвы движется по рабочей поверхности клина, не изменяя длины и толщины а. Сопротивлением изгибу пласта при поступлении на клин пренебрегаем. Направления сил G и RG известны, а направление действия силы QG принимаем параллельно оси ОХ.
Рисунок 4.5 - Схема сил, действующих на клин без учета сил трения
Проектируя эти силы на оси координат ОХ и ОZ, находим
Откуда QG = G×; tgα;. (2) Сила тяжести пласта, находящегося на клине G =a ×; b ×; l ×; γоб ×; g, (3) где а – глубина хода клина, м; b – ширина захвата клина, м; l – длина рабочей поверхности клина АВ, м; γоб - объемная масса почвы, Сила сопротивления клина для преодоления статистического давления пласта, обусловленного его силой тяжести: RGX = QG = G ×tgα;, (4) или с учетом выражения (3) RGX = a ×; b ×; l ×; γоб ×; g ×; tgα;. (5) Подставив условия задачи в выражения (5), получим: RGX =0,2∙0,7∙0,3∙1400∙9,8∙tg20° =209,8 H. Ответ: RGX =209,8 H.
Пример 11. Определить горизонтальную составляющую тягового сопротивления двухгранного клина от силы тяжести пласта и сил трения, возникающих при скольжении пласта по рабочей поверхности клина. Известны: Решение: Приведем расчетную схему (рисунок 4.6)
Рисунок 4.6 - Схема сил, действующих на клин с учетом сил трения
На пласт действует реакция недеформированной почвы, находящейся впереди клина, QG; сила тяжести пласта G и результирующая элементарных нормальных сил сопротивления почвы и сил трения на рабочей поверхности клина RG. Аналогично предыдущей задаче допустим, что пласт почвы движется по клину, не изменяя длины и толщины. Пренебрегаем также сопротивлением изгибу пласта при поступлении его на клин. Направление действия силы QG принимаем параллельно оси OX. Проектируя эти силы на оси координат, OX и OZ находим:
Откуда QG = G×; tg(α+φ). (2) Поскольку G =a ×; b ×; l ×; γоб ×; g, то Подставив условия задачи в выражения (3), получим: RGX =0,2∙0,7∙0,3∙1400∙9,8∙tg(20° + 46°)=596,9 H. Ответ: RGX =596,9 Н.
Пример 12. Определить горизонтальную составляющую тягового сопротивления двугранного клина от динамического давления пласта почвы, обусловленного силой инерции. Известны: Решение: Динамическое давление пласта почвы Fд на рабочую поверхность клина, обусловленное силой инерции пласта, можно рассматривать как непрерывный удар частиц почвы о плоскость клина. Поэтому на основании теоремы изменения количества движения
где υ1 – начальная скорость частиц почвы до их соприкосновения с клином υ1 =0, υ;а – абсолютная скорость движения пласта, м/с. Значенеие скорости υ;а может быть определено из треугольника скорости (рисунок 4.7), поскольку при обработке влажной задернелой почвы пласт обычно имеет вид сплошной ленты и усадки не происходит. Поэтому относительная скорость движения пласта υr равна скорости поступательного движения клина υ;. Следовательно:
Так как начальная скорость υ1 = 0, то уравнение (1) примет вид:
Массы почвы
Рисунок 4.7 - Схема сил, действующих на клин от динамического давления пласта почвы
Подставляя выражение (4) и (2) в уравнение (3), получим:
Сила Fд (см. рисунок 4.7) приложена к рабочей поверхности клина близ лезвия, так как именно в начале поступления почвы на клин он сообщает ей ударный импульс, в результате которого почва начинает двигаться с постоянной скоростью υ;а. Сила Fд уравновешивается реактивной силой RF, отклоненной на угол φ; от нормали к поверхности клина, и подпором QF почвы, находящийся впереди клина. Направление QF можно с некоторым допущением принять горизонтальным [8]. Проекция силы Rд на оси координат ZOY
Выразив RFX и RFZ соответственно через
и решая совместно выражения (6) с учетом (5), получим:
Подставляя условия задачи в выражение (7), находим
Ответ: RFX =283 Н.
Пример 13. Определить горизонтальную составляющую силы сопротивления снятию почвы затупленным лезвием клина. Если известны: b =0,7 м; q0 =10 Н/см3; высота затылочной фаски h =5мм; угол затылочной фаски ε;з=300; угол трения почвы φ;=260. Решение: Сопротивление смятию почвы затупленным лезвием клина (см. рисунок 4.4) можно определить по выражению (4.12). Горизонтальная составляющая силы сопротивления смятию почвы определится по выражению
Подставляя условия задачи в выражение (7), получим
Ответ: Rзх =173,5 Н.
Пример 14. Определить общую величину тягового сопротивления двугранного клина по условиям примеров 11,12 и 13 без учета силы сопротивления на деформацию почвы. Решение: Общая величина тягового сопротивления без учета силы сопротивления на деформацию почвы Rд: Рx = Rзx + RGx + RFx =596,9+283+173,5=1053,4 Н. Ответ: Рx =1053,4 Н.
Пример 15. Определить наибольшую длину рабочей поверхности клина, если заданы: Решение: Наибольшая величина реакции недеформированной почвы Q =a∙b∙ σсж, (1) где σсж – временное сопротивление почвы сжатию, кПа. Реакция недеформированной почвы складывается из QG и QF (см. примеры 11 и 12). Поэтому Q = QG + QF. (2) Поскольку при решении примера 11 определили, что QG = RGX =a×b×l×γоб×g×tg(α+φ), (3) а при решении примера 12 нашли, что
то
где Подставляя выражения (3) и (5) в уравнение (2), получим
С учетом выражения (1) последнее (6) примет вид
Отсюда
Подставляя исходные данные в полученную зависимость (8) получим:
Ответ: l = 5,4 м.
|

 .
.
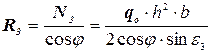 , (4.12)
, (4.12) , (4.13.)
, (4.13.) , длина рабочей поверхности клина l =0,3 м, ширина захвата клина b =0,7 м, глубина хода клина а =0,2 м, рабочий угол клина α;=200. Силой трения о поверхность клина пренебречь.
, длина рабочей поверхности клина l =0,3 м, ширина захвата клина b =0,7 м, глубина хода клина а =0,2 м, рабочий угол клина α;=200. Силой трения о поверхность клина пренебречь.
 . (1)
. (1)
 ; g – ускорение свободного падения, м/с2.
; g – ускорение свободного падения, м/с2.
 . (1)
. (1) ,
, (3)
(3) (1)
(1) (2)
(2) (3)
(3) , поступающей на клин в единицу времени
, поступающей на клин в единицу времени
 (4)
(4) (5)
(5)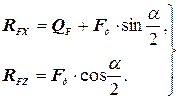 (6)
(6)

 (7)
(7)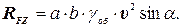 (8)
(8)
 (7)
(7)
 (5)
(5)
 (6)
(6) (7)
(7) (8)
(8)



