Упражнения. 1.25. Построить профиль борозды и определить угол наклона δ нижней грани отваленного пласта, если глубина вспашки а
1.25. Построить профиль борозды и определить угол наклона δ; нижней грани отваленного пласта, если глубина вспашки а, а ширина пласта b.
1.26. Определить, при какой глубине отваленный пласт окажется неустойчивым, если вспашка производится корпусом с шириной захвата b =0,25 м; b =0,35 м; b =0,4 м.
1.27. Построить профиль борозды и определить угол наклона отваленного пласта при работе c предплужником, если глубина вспашки а, ширина пласта b, глубина вспашки предплужника а1 и ширина захвата его b1
1.28. Определить тип цилиндроидальной рабочей поверхности корпуса плуга имеющего углы γ0 и γmax
1.29. Определить максимальную глубину пахоты корпусом с шириной захвата b и угол поворота пласта связной почвы, когда он займет устойчивое положение. Вспашка производится поперек склона крутизной α;.
Указание: Использовать формулу (1) примера 19
1.30. Определить радиусы Rmi n и Rmax направляющей кривой культурного отвала при следующих исходных данных: ширина захвата корпуса плуга b, глубина пахоты а, угол ε;0 и угол γ0.
1.31. Произвести расчет и построить график для образующих культурного отвала с параметрами γ0, γmin, γmax.
1.32. Определить площадь (теоретическую) неровностей поверхности на участке (S =1 га), образованную после вспашки плугом ПЛН-4-35 на глубину а (Указание: при решении задачи использовать схему, приведенную на рисунке 4.8).
1.33. Определить объем (теоретический) неровностей, образованный после вспашки плугом ПЛН-4-35 на глубину а и количество жидких атмосферных осадков, накапливаемых на участке площадью S =1 га без учета воды на инфильтрацию.
1.34. Определить площадь (теоретическую) неровностей поверхности участка (S =1 га), расположенного на склоне крутизной α;, и образованную после вспашки поперек склона плугом ПЛН-4-35 на глубину а (Указание: при решении задачи использовать схему, приведенную на рисунке 4.10).
1.35. Определить объем (теоретический) неровностей, образованный после вспашки плугом ПЛН-4-35 на глубину а и количество жидких атмосферных осадков, накапливаемых на участке площадью S =1 га без учета воды на инфильтрацию.
1.36. Определить площадь и объем (теоретические значения) неровностей, образованные после вспашки поперек склона плугом ПЛН-4-35 на глубину а при отваливании пласта вверх и вниз по склону на площади участка S =1 га.
4.1.5. Рациональная формула В.П. Горячкина для определения тягового сопротивления плуга
Для определения силы, необходимой для тяги плуга, основоположник земледельческой механики академик Василий Прохорович Горячкин предложил формулу, раскрывающую закономерности и физическую связь между основными факторами рабочего процесса плуга и общим сопротивлением, возникающим при его работе. Эти зависимости записаны в рациональном виде, отсюда сама формула, названная рациональной, имеет вид
где Коэффициент полезного действия плуга
Определение коэффициентов f, k и ε; рациональной формулы В.П. Горячкина производиться по формулам:
где Расчетное усилие на плуг определяется по выражению
где ν; – коэффициент увеличения среднего тягового сопротивления Рх, принимаемый для 2-х и 3-х корпусных плугов ν; ≤2, для 4-х корпусных плугов ν; ≤1,8, для 5-и корпусных плугов ν; ≤1,5. Расчетное усилие на один корпус рекомендуется определять по выражению:
где n – число корпусов плуга. Расстояние от носка лемеха до пятки полевой доски (технологическая длина) для обеспечения устойчивого хода плуга в горизонтальной плоскости может быть определена по формуле:
где ln – расстояние от носка лемеха до пятки полевой доски (технологическая длина); φ; – угол трения почвы о полевую доску; γ0 – угол постановки лезвия лемеха к стенке борозды; b – ширина захвата корпуса плуга. Ширина полевой доски ап может быть определена по выражению
где Rxy – равнодействующая проекция на горизонтальную плоскость элементарных сопротивлений почвы, возникающих на рабочей поверхности корпуса и лезвии лемеха; q0 – коэффициент объемного смятия почвы; l1 – длина полевой доски; ξ; – угол постановки полевой доски к стенке борозды, ξ;=2…3°. Пример 23. Определить коэффициенты рациональной формулы академика В.П. Горячкина по результатам шести измерений (пример взят из работ профессора Н.Д. Лучинского).
Решение: В целях удобства вычислений можно рекомендовать данные динамометрированния и вычисления величин m, l, q и r по формулам (4.21) и (4.22) расположить в таблице 4.5.
Таблица 4.5 - Расчетные данные
Используя расчетные формулы (4.20), (4.21) и (4.22), исходные данные и расчетные данные (см. таблицу 4.4), получим:
Ответ:
Пример 24. Пятикорпусный полунавесной плуг, имеющий массу 1200 кг и ширину захвата каждого корпуса 0,35 м, пашет на глубину 0,22 м со скоростью 2 м/с. Определить среднее тягового сопротивление этого плуга, если коэффициенты рациональной формулы В.П. Горячкина: Решение: Подставив исходные данные в формулу (4.18), получим:
Пример 25. По условиям примера 24 определить коэффициент полезного действия плуга. Решение: Используя расчетную формулу (4.19) и исходные данные предыдущего примера, получим:
Ответ: η;=0,738.
Пример 26. Для полунавесного плуга ПЛП-6-35, работающего в пятикорпусном варианте определить расчетное усилие на плуг и расчетное усилие на один корпус, если G =12 кН; Решение: Используя расчетные формулы (4.18), (4.23), (4.24) и исходные данные, получим:
Ответ: Ррасч = 42,87кН;
Пример 27. Определить расстояние от носка лемеха до пятки полевой доски (технологическая длина) для корпуса плуга ПЛН-4-35 при вспашке почвы, имеющей коэффициент трения по отвалу Решение: Для устойчивого хода плуга в горизонтальной плоскости, по крайней мере, необходимо, чтобы равнодействующая сила Rxy при продолжении пересекала в пятке (точка В) полевую доску (рисунок 4.14). Из треугольника ∆ ADB по теореме синусов можно записать:
Рисунок 4.14 - К обоснованию расстояния от носка лемеха до пятки полевой доски
Поскольку
Подставив в выражение (4.25) исходные данные задачи, получим:
где Ответ: ln =0,747 м.
Пример 28. Определить ширину полевой доски корпуса плуга, если равнодействующая проекция на горизонтальную плоскость элементарных сопротивлений, возникающих на рабочей поверхности корпуса и лезвии лемеха, равна 7,5 кН, q0 =10 Н/см3, γ0 =40°, φ;=30°, ξ;=2°, l1 =0,33 м. Решение: Ширина полевой доски aп (см. рисунок 4.14) может быть определена из выражения (4.26). Подставив в выражение (4.26) исходные данные задачи, получим:
Ответ: аn= 0,0906 м.
|

 (4.18)
(4.18)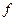 - коэффициент, аналогичный коэффициенту трения; G – сила тяжести плуга, Н; k - коэффициент удельного сопротивления почвы, Па; а и b – размеры сечения пласта, м; ε; – размерный коэффициент, зависящий от формы отвала и свойств почвы, Н∙с2∙м-4; υ; – скорость, м/с; n – число корпусов плуга.
- коэффициент, аналогичный коэффициенту трения; G – сила тяжести плуга, Н; k - коэффициент удельного сопротивления почвы, Па; а и b – размеры сечения пласта, м; ε; – размерный коэффициент, зависящий от формы отвала и свойств почвы, Н∙с2∙м-4; υ; – скорость, м/с; n – число корпусов плуга.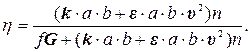 (4.19)
(4.19) , (4.20)
, (4.20) (4.21)
(4.21) (4.22)
(4.22) ;
;  ;
;  ;
; 
 .
. , (4.23)
, (4.23)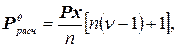 (4.24)
(4.24) , (4.25)
, (4.25)
 (4.26)
(4.26)


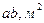

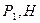
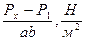

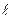 =36,55
=36,55





 Ответ: 22,441кН.
Ответ: 22,441кН.
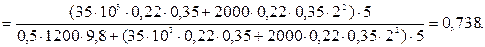
 k =48,8кН/м2; ε;=2,54 кН∙с2/м4; υ;=1,5 м/с; а =0,2 м.
k =48,8кН/м2; ε;=2,54 кН∙с2/м4; υ;=1,5 м/с; а =0,2 м. Px =28,58кН
Px =28,58кН кН; Ррасч = 42,87кН.
кН; Ррасч = 42,87кН.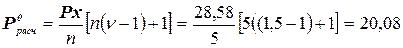 кН.
кН. .
. , если угол между лезвием лемеха и стенкой борозды равен 40°.
, если угол между лезвием лемеха и стенкой борозды равен 40°.

 и
и 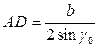 , то получим выражение (4.25):
, то получим выражение (4.25): . (4.25)
. (4.25) м,
м,
 м
м


