Упражнения. 1.65. Определить величину затылочного угла εa для диска бороны диаметром D=510 мм, радиусом сферы R=600 мм
1.65. Определить величину затылочного угла εa для диска бороны диаметром D =510 мм, радиусом сферы R =600 мм, глубине хода а, угле атаки α; и угле заострения i. Решение сопроводить расчетной схемой.
1.66. Определить максимальную глубину хода дисков лущильника со следующими параметрами: диаметр диска D, радиус сферы R, угол атаки α и угол заострения i. Решение сопроводить расчетной схемой.
1.67. Определить расстояние между дисками лущильника с указанными в задаче 1.66 параметрами D и α;. Высоту гребней принять с1 =30 мм и с2 =35 мм.
1.68. Определить величину перекрытия дисков на уровне поверхности поля в поперечном направлении движения агрегата, если известны: расстояние между смежными дисками b, угол атаки α;, диаметр диска D и глубина хода а.
1.69. Определить высоту гребней с, полученных после обработки почвы дисковым лущильником, установленным под углом атаки α;, если диски имеют диаметр D и расстояние между смежными дисками b =17 см. Решение сопровождать расчетной схемой.
1.70. Определить тяговое сопротивление одиночного сферического диска при следующих условиях: коэффициент удельного сопровождения почвы k, диаметр диска D, угол атаки α; и глубина обработки а.
4.1.10. Ротационные почвообрабатывающие рабочие органы с активным приводом
Рабочие органы фрез совершают сложное движение: поступательное со скоростью υм агрегата и вращательное со скоростью ω; вокруг оси барабана:
где R – радиус барабана, м. Кинематический показатель режима работы фрезы определяют по формуле:
Подача на нож фрезы представляет собой путь, пройденный машиной за время поворота фрезерного барабана на угол между соседними ножами
где z – число ножей, вращающихся в одной плоскости. При работе фрезы на дне борозды образуются гребни (см. рисунок 4.20), высота с которых зависит от величины подачи xz и режима работы фрезы λ;. Теоретически можно для фрезы при допустимой величине с определить значение λ; по формуле
где z – число ножей, вращающееся в одной плоскости. Приближенно наибольшую толщину стружки δ; можно вычислить по формуле [7,8]:
где
Пример 45. Определить абсолютную скорость υ;а ножа в момент входа его в почву, если известны скорость перемещения машины υ;м, радиус фрезерного барабана R, глубина обработки a и кинематический показатель режима работы λ;. Решение сопроводить расчетной схемой. Решение: Приведем расчетную схему (рисунок 4.20).
Рисунок 4.20 - Траектория движения точки рабочего органа фрезы Координаты точки А1 по отношению к неподвижным осям x и y будут:
Продифференцируем уравнение (1) по времени t
Отсюда абсолютная скорость, т.е. скорость резания
С учетом формулы (4.43) выражение (3) перепишется
Из второго уравнения системы (1) можно получить
Подставив (5) в выражение (4) получим:
Из полученного выражения (6) следует, что абсолютная скорость υa ножа в момент его входа в почву зависит от поступательной скорости υ;м машины, кинематического режима работы фразы λ;, радиуса фрезерного барабана R и глубины обработки а. Ответ:
Пример 46. Определить основные конструктивные параметры фрезы, которая комплектуется жесткими Г-образными ножами, если подача на нож фрезы xzmax= 0,1 м, а глубина обработки до 0,15 м. Решение: Расчет ведем по максимальной глубине обработки аmax =0,15 м. Принимаем из конструктивных соображений [8, с. 298]: R=1,5 аmax,с=0,2 аmax . Поскольку на каждом диске поочередно установлены левые и правые ножи, а в формулах (4.44) и (4.45) подразумевается под z число ножей, вращающихся в одной плоскости, то при общем числе ножей, равным четырем число ножей будет z =2, при шести – соответственно z =3. Для предотвращения чрезмерно большой подачи xz примем z =3. Подставляя в выражение (4.45) значения R=1,5аmax, с=0,2аmax и z =3, находим
λ;=3,14. Для определения подачи xz воспользуемся выражением (4.44), подставив в нее λ;=3,14; R=1,5аmax =0,225 м и z =3, имеем:
Найденная величина xz превышает заданную xzmax=0,1 м. Следовательно, принятое значение λ;=3,14 должно быть изменено. Из выражения (4.44) определим λ; при xz =0,1 м, z =3 и R=1,5аmax =0,225 м:
Поскольку увеличение λ; при постоянных значениях z =3 и R=1,5×аmax вызывает уменьшение высоты гребня с, то есть повышает качество производимой работы, то найденное значение λ;=4,71 может быть принято для дальнейших расчетов. Определим высоту с гребня, соответствующую новому значению λ; по формуле (4.45), методом последовательных приближений: с =0,06∙0,15=0,009 м. Принимая υ;м =1,5 м/с, определим окружную скорость фрезерного барабана
Отсюда частота вращения барабана
Ответ: R =0,225 м; λ;=4,71; с =0,009 м; υ; =1,5 м/с; z =3.
|

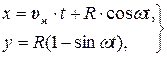 (4.42)
(4.42) (4.43)
(4.43) , (4.44)
, (4.44)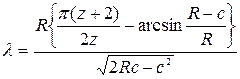 , (4.45)
, (4.45) , (4.46)
, (4.46) - отношение глубины обработки к радиусу фрезбарабана. Практически для получения качественного рыхления рекомендуется величину m принимать m =0,7…0,8.
- отношение глубины обработки к радиусу фрезбарабана. Практически для получения качественного рыхления рекомендуется величину m принимать m =0,7…0,8.
 (1)
(1) (2)
(2) (3)
(3) (4)
(4) . (5)
. (5) (6)
(6)
 .
.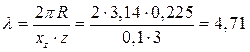 .
.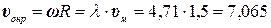 м/с
м/с мин-1.
мин-1.


