Пусть y явл. ф-й от х. Известны лишь некоторые значения 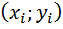 , т.е дискретному множеству
, т.е дискретному множеству  поставлено в соотв. дискретное множество
поставлено в соотв. дискретное множество 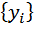 – функция задана таблично. Ставится задача отыскания значения ф-и y в других точках, отличных от узлов
– функция задана таблично. Ставится задача отыскания значения ф-и y в других точках, отличных от узлов  . Этой цели и служит задача о приближении или аппроксимации ф-ции, заданной дискретно.
. Этой цели и служит задача о приближении или аппроксимации ф-ции, заданной дискретно.
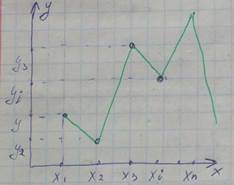 Линейная интерполяция: она состоит в том, что заданные точки
Линейная интерполяция: она состоит в том, что заданные точки 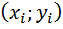 соединяются прямолинейными отрезками и функция S(x) приближается к ломанной, с вершинами в данных точках. Для i-го интервала можно написать ур-е прямой, проходящей через точки
соединяются прямолинейными отрезками и функция S(x) приближается к ломанной, с вершинами в данных точках. Для i-го интервала можно написать ур-е прямой, проходящей через точки 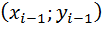 и
и 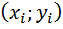
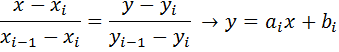
Таким образом, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента х, а затем построить ур-е прямой по двум точкам, концами этого интервала, и найти значение y(x).
 Квадратичная интерполяция: в качестве интерполяционной функции на отрезке
Квадратичная интерполяция: в качестве интерполяционной функции на отрезке  принимается квадратный трехчлен. Ур-е кв. трехчлена
принимается квадратный трехчлен. Ур-е кв. трехчлена  при
при  , которое содержит 3 неизв. коэффициента -
, которое содержит 3 неизв. коэффициента - 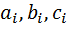 . Для их определения необходимо 3 уравнения. Ими служат условия прохождения параболы через 3 точки -
. Для их определения необходимо 3 уравнения. Ими служат условия прохождения параболы через 3 точки -  , которые можно записать в виде:
, которые можно записать в виде:
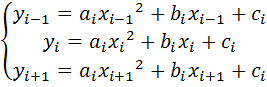
Решая эту систему лин. ур-й относительно 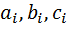 , мы найдём коэффициенты квадратного трехчлена.
, мы найдём коэффициенты квадратного трехчлена.
Многочлен Лагранжа
Ln(x)=  , где pui(x)=
, где pui(x)=  ,i=0,1,…,n
,i=0,1,…,n
Многочлен Ньютона
N(xi+th)=yi+t∆yi+  ; i=0,1,…,n
; i=0,1,…,n

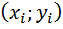 , т.е дискретному множеству
, т.е дискретному множеству  поставлено в соотв. дискретное множество
поставлено в соотв. дискретное множество 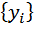 – функция задана таблично. Ставится задача отыскания значения ф-и y в других точках, отличных от узлов
– функция задана таблично. Ставится задача отыскания значения ф-и y в других точках, отличных от узлов  . Этой цели и служит задача о приближении или аппроксимации ф-ции, заданной дискретно.
. Этой цели и служит задача о приближении или аппроксимации ф-ции, заданной дискретно. Линейная интерполяция: она состоит в том, что заданные точки
Линейная интерполяция: она состоит в том, что заданные точки 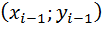 и
и 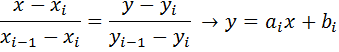
 Квадратичная интерполяция: в качестве интерполяционной функции на отрезке
Квадратичная интерполяция: в качестве интерполяционной функции на отрезке  принимается квадратный трехчлен. Ур-е кв. трехчлена
принимается квадратный трехчлен. Ур-е кв. трехчлена  при
при  , которое содержит 3 неизв. коэффициента -
, которое содержит 3 неизв. коэффициента - 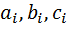 . Для их определения необходимо 3 уравнения. Ими служат условия прохождения параболы через 3 точки -
. Для их определения необходимо 3 уравнения. Ими служат условия прохождения параболы через 3 точки -  , которые можно записать в виде:
, которые можно записать в виде: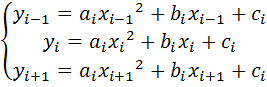
 , где pui(x)=
, где pui(x)=  ,i=0,1,…,n
,i=0,1,…,n ; i=0,1,…,n
; i=0,1,…,n


