Эмпирические формулы.
Пусть изучая неизвестную функцию. Зависимость y(x). Мы в расчете серии экспериментов получили таблицу значений.
Задача состоит в том, чтобы найти зависимость y=f(x), значение которого при x=xi мало отличается от опытных данных yi. Построенная т.о. ф-ла y=f(x) называется эмпирической. Задача на построение эмпирической формулы отличается от задач интерполирования тем, что график эмп. зависимости не проходит через узлы (xi; yi), что приводит к сглаживанию эмпирических данных, а интерполяционная формула повторила все ошибки эксперимента. Построение эмп ф-лы сост из 2-х этапов: 1) Подбор общего вида ф-лы 2) Опред наилучших значений содержащихся в ней параметров Виды эмп ф-л: 1) Линейная зависимость y=ax+b (легко видеть после построения графика) 2) Степенная зависимость 3) Показательная зав-ть 4) Гиперболическая Для определения параметров эмпир ф-лы, сущесв след метода: 1) Метод выбранных точек: пусть для с-мы определенных точек Mi(xi;yi) выбрана эмпир ф-ла y=f(x;a1,a2….an) На корд пл-ти XOY проводится плоская кривая Г опис точки Mi. На линии Г выбир с-мы из M точек с корд Nj 2) Метод средних. Если в эмпир т-ру подставить исход данные Mi(xi;yi) то левая и правая части будут не равны. Разности ε=f(xi; a1…an)-yi называют упрощениями и предст собой расстоянию вертикали т. Mi от графика. Согласно методу средних за наилучшее положение Г приним то. для которых Зам: метод наим квадр обл тем преимуществом. Что если сумма квадратов мала, то сами уклонения тоже малы. Необходимое условие существования эмпир ф-мы: пусть например
|

 (м.б. сведена к линейной)
(м.б. сведена к линейной) 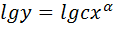 U=lny
U=lny 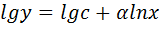 Ù=lnα U=α Ù+β β=lgc
Ù=lnα U=α Ù+β β=lgc также м.б. сведена к линейной.
также м.б. сведена к линейной.
 , равноудаленных друг от друга. Параметры а1…аn м.б. найдены из с-мы ур-ний:
, равноудаленных друг от друга. Параметры а1…аn м.б. найдены из с-мы ур-ний: 
 . Для опред по методу ср постоянных a1…am счит те, для которых сумма квадратов минимальна S(a1…am)=
. Для опред по методу ср постоянных a1…am счит те, для которых сумма квадратов минимальна S(a1…am)=  2 Отсюда исп необход условие экстремума ФНП получаем:
2 Отсюда исп необход условие экстремума ФНП получаем:  Если сумма имеет единств решение то оно будет искомым.
Если сумма имеет единств решение то оно будет искомым. выберем
выберем  вычислим y:
вычислим y:  ;
;  ;
;  ,=>
,=> 
 т.о. для существ степени завис
т.о. для существ степени завис 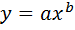 необходимо чтобы среднему геом xs значений x1xn соотв ys знач y1yn, т.е. если xi образует геом прогрессию, то значение yi также должны образ геом прогрессию.
необходимо чтобы среднему геом xs значений x1xn соотв ys знач y1yn, т.е. если xi образует геом прогрессию, то значение yi также должны образ геом прогрессию.


