Погрешность (задачи, метода, округлений). Абсолютная и относительная погрешность. Понятие устойчивости, корректности, сходимости.
Погрешность (задачи, метода, округлений). Абсолютная и относительная погрешность. Понятие устойчивости, корректности, сходимости. При решении мат. задач почти неизбежно появление погрешностей 3 типов: - погрешность задачи – связана с приближенным характером исходной содержательной модели, с невозможностью учесть все факторы в процессе изучение моделируемого явления. Для вычислителя погрешность задачи след. считать неустранимой или безусловной; - погрешность метода – связана со способом решения поставленной математической задачи, и появляющаяся в результате подмены исходной математической модели другой. При создании численных методов закладывается возможность отслеживания и доведения их до сколь угодно малого уровня -> отношение погр. метода как к устранимой или условной; - погр. округлений – обусловлена необходимостью выполнять арифметические операции над числами с усеченными до количества разрядов, зав. от применения вычислительной техники; Эти погрешности в сумме дают полную погр. решения задачи. Пусть А и а – два близких числа. Условимся считать А – точным, а – приближенным. Величина Устойчивость: пусть по исходному значению величины х находится значение величины у, если исходная величина имеет абсол. порг. Корректность: задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса её решение существует единственно и устойчиво по исходным данным. Сходимость: означает близость получаемого численного решения задачи к истинному.
|

 – абсолютная погрешность;
– абсолютная погрешность;  Числа
Числа  называются оценками абсол. И относ. погрешностей.
называются оценками абсол. И относ. погрешностей.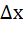 , то решении имеет погр.
, то решении имеет погр. 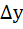 . Задача называется устойчивой по исходному параметру х, если решение у непрерывно от него зависит, т.е
. Задача называется устойчивой по исходному параметру х, если решение у непрерывно от него зависит, т.е 



