Решение линейных систем. Норма (матрицы, вектора) и понятие обусловленности. Прямые и итерационные методы решения.
Рассмотрим линейную алгебраическую систему, записанную в виде векторно-математ. уравнения
b – ненулевой n-мерный вектор Пусть правая часть (1) получила приращение
Норма (матрицы, вектора) А - действительное число 1. 2. 3. Длина вектора и есть норма, обратное не верно. Норма вектора – выражение вида При p=2: При p=1: При p= Обусловленность - положительное число
Методы решения систем линейных уравнений делятся на прямые и итерационные. Прямые – используют конечные разности для вычисления неизвестных. Просты и наиболее универсальны. Недостатки – требуют хранения в памяти ЭВМ сразу всей матрицы, не учитывают структуру матрицы, сильное накапливание погрешностей в процессе решения. Итерационные – методы последовательных приближений, в которых необходимо задать начальное приближение и после этого с помощью некоторого алгоритма проводится один цикл вычислений – итерация. Итерации проводятся для получения решений с треб. точностью. «+» - не треб. хранения в памяти машины всей матрицы, погрешности не накапливаются.
|
; А – невырожденная матрица (квадратная матрица, определитель которой отличен от нуля) nxn;
; x – n-мерный вектор неизвестных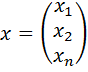 
;
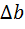, т.е вместо истинного вектора b воспользуемся 
. Реакцией решения х на возмущение 
, т.е если х – решение (1), то
– решение 
. Для того, чтобы сравнивать и оценивать близость матриц (векторов), вводится понятие нормы: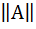
(норма А), удовлетворяющее условиям:
: 
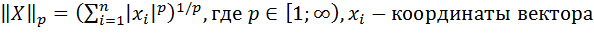
(мера обусловленности) матрицы А. Обозначают condA;
