Решение нелинейных уравнений. Методы деления отрезка пополам, хорд, касательных, простой итерации.
Пусть требуется решить уравнение F(x) = 0, прямые методы позволяют записать корни в виде некоторого конечного соотношения, но большинство уравнений не могут быть решены прямым методом. Для их решения используют итерацион. Методы. Алгоритм нахождения корня ур-я с помощью итер. метода состоит из двух этапов: 1. Отыскание приближенного значения корня или содержащего его отрезка; 2. Уточнение приближенного значения до некоторой заданной степени точности.
Метод деления отрезка пополам
После n-й итерации отрезок сокращается в
Пусть на отрезке Через точки
Находим точку пересечения с осью абсцисс, т.е (у=0)
Сравниваем знаки F(a), F(b), F(c0), выбираем интервал, знаки на концах которых разные [c0;b], затем проводится след. итерация
Его отличие от предыдущего состоит в том, что проводится касательная к графику ф-и F(x). Тогда С0 – некое начальное приближение. Строят уравнение касательной (y=0) Простая итерация Если удалось уравнение F(x)=0 переписать в виде x=f(x), то выбрав начальное приближение С0 можно построить итерационный процесс Сn+1 = f(Cn). Достаточным условием сходимости этого метода явл. условие
|

 Приближенное значение корня может быть найдено различным способами: из физических соображений, из решения аналогичной задачи, с помощью графических методов. Если такие априорные оценки исходного приближения найти не удаётся, то находят 2 близко приближенные точки a и b, в которых непрерывная функция F(x) принимает значения разных знаков.
Приближенное значение корня может быть найдено различным способами: из физических соображений, из решения аналогичной задачи, с помощью графических методов. Если такие априорные оценки исходного приближения найти не удаётся, то находят 2 близко приближенные точки a и b, в которых непрерывная функция F(x) принимает значения разных знаков.  . В этом случае м/ж точками a и b есть по крайней мере одна точка, в которой F(x)=0. В качестве нач. прибл-я
. В этом случае м/ж точками a и b есть по крайней мере одна точка, в которой F(x)=0. В качестве нач. прибл-я  можно взять середину отрезка [a;b], т.е
можно взять середину отрезка [a;b], т.е 



 раз. Итер. процесс продолжается до тех пор, пока значении ф-и F(x) после n-й итерации не станет меньше по модулю заданного числа Ԑ:
раз. Итер. процесс продолжается до тех пор, пока значении ф-и F(x) после n-й итерации не станет меньше по модулю заданного числа Ԑ:
 Метод хорд
Метод хорд существует корень, т.е
существует корень, т.е  и
и  проводим прямую, каноническое уравнение которой имеет вид:
проводим прямую, каноническое уравнение которой имеет вид:


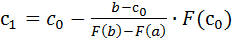 и т.д. Итер. процесс продолжается до тех пор, пока
и т.д. Итер. процесс продолжается до тех пор, пока  или
или 
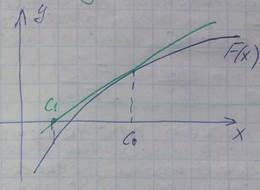 Метод касательных
Метод касательных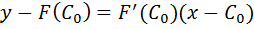 , откуда находим след. приближение корни С1, как абсциссу точки пересечения касательной с осью Х.
, откуда находим след. приближение корни С1, как абсциссу точки пересечения касательной с осью Х. . Аналогично нах-ся след. приближение
. Аналогично нах-ся след. приближение 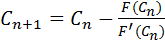 . Для окончания итер. процесса м.б. использовано условие
. Для окончания итер. процесса м.б. использовано условие 



