Нахождение двугранных углов
| |
|
|
| | | Решите задачу
| Решите задачу
| Решите задачу
| | *
| Основание пирамиды SABC – прямоугольный треугольник с прямым углом B, SO – высота пирамиды. Построить ЛУДУ при ребрах AB и BC.
| Через вершину квадрата АВСD проведён к его плоскости перпендикуляр DМ равный 10см. Угол между плоскостями АВС и MDC равен 45º. Найти площадь треугольника ВСM
| Через вершину D тупого угла ромба АВСD проведен перпендикуляр DK равный 9 см. Диагонали ромба равны 12 см и 16 см. Вычислить углы между плоскостями АВС и KВС
| |
| Основание пирамиды MNPK-прямоугольный треугольник NPK с прямым углом К. Высота МО падает в центр описанной окружности. Постройте ЛУДУ при ребрах NK и PK.
| Отрезки АС и ВС, лежащие в гранях прямого двугранного угла перпендикулярны к его ребру. Вычислите расстояние между точками А и В, если АС=10 см, ВС=24 см
| Дан треугольник MNP, у которого угол М равен 90º; MN=9 см. Через сторону РМ проведена плоскость α под углом 60º к плоскости треугольника MNP. Найти расстояние от вершины N до плоскости α.
| |
| Основанием пирамиды SABCD является квадрат. Высота SO падает в точку пересечения диагоналей. Построить ЛУДУ при ребрах АВ и ВС.
| Точка К, лежащая в грани двугранного угла удалена от другой грани на 12 см, а от ребра на 8  см. вычислите величину двугранного угла. см. вычислите величину двугранного угла.
| Катет прямоугольного треугольника APN с прямым углом N лежит в плоскости α, а угол между плоскостями α и APN равен 60º. Найти расстояние от точки Р до плоскости α, если AN=12 см, АР=13 см.
| |
| Основание пирамиды SABC – треугольник, у которого AB=BC, высотой служит ребро SB. Построить линейный угол двугранного угла при ребре AC.
| В грани двугранного угла равного 30º расположена точка A. Вычислить расстояние от точки A до второй грани, если она удалена от ребра двугранного угла на 16 см.
| Правильные треугольники ABC и DBC расположены так, что вершина D проектируется в центр треугольника ABC. Найти угол между плоскостями этих треугольников.
| |
| Основание пирамиды SABC – прямоугольный треугольник с прямым углом ABC, SO – высота пирамиды. Построить линейные углы двугранных углов при ребрах AB и BC.
| Угол между плоскостями α и β равен 60º. Точка С принадлежит ребру этого угла, отрезки АС и ВС перпендикулярны этому ребру и равны соответственно 5 см и 8 см. Вычислить расстояние между концами этих перпендикуляров.
| Через сторону AB треугольника ABC проведена плоскость α, расстояние от вершины C до плоскости α равно 7,5 см. Найти угол между плоскостью α и плоскостью треугольника, если AB=16 см., AC=BC=17 см.
|
| |
| 2
|
| |
| Основание пирамиды SABC правильный треугольник, SO-высота. Постройте линейные углы двугранных углов при ребрах основании пирамиды.
| Внутри прямого двугранного угла взята точка А, удаленная от его граней на 12 см и 16 см. Вычислите расстояние от точки А до ребра двугранного угла.
| Двугранный угол между плоскостями треугольников MNP и MNK равен 60º. Найти РК, если МК=NK=5см, MN=6см, MP=NP=3 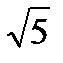 см. см.
| |
| Основанием пирамиды является прямоугольник. АВСD. Высота SO падает в точку пересечения диагоналей. Постройте ЛУДУ при ребрах BC и CD.
| На ребре двугранного угла, равного 180º расположена точка А. В его гранях проведены перпендикуляры к ребру АВ и ВС, равные соответственно 10 см и 8 см. Найти расстояние между точками В и С.
| Точка К удалена от каждой стороны равностороннего треугольника АВС на 8 см; АВ=24 см. Найти величину двугранного угла с ребром ВС, грани которого содержат точки К и А.
| |
| Основание пирамиды SABCD-равнобедренная трапеция, у которой АD//ВС. Величина пирамиды проецируется в середину ребра АД. Построить ЛУДУ при ребре ВС.
| Через вершину квадрата АВСД проведён к его плоскости перпендикуляр РК равный 10см. Угол между плоскостями АВС и RDC равен 45. Найти площадь треугольника ВСК
| Сторона (АВ) квадрата АВСД лежит в плоскости. Прямая СД удалена от этой плоскости на 18см. ВС=36см.Вычислите угол между плоскостью квадрата и плоскостью
| |
| Основание пирамиды SАВС прямоугольный треугольник АВС с прямым углом С. Высота Sо падает в центр описанной окружности. Построить линейные углы двугранных углов при рёбрах АС и ВС
| Через вершину острого угла прямоугольного треугольника АВС проведён перпендикуляр АД к его плоскости. АД=6см; АСВ=90; АВС=30. Угол между плоскостями DCL и АВС равен 60. Найти длины ДС и ДВ.
| Через центр О квадрата АВСД проведён к его плоскости перпендикуляр КО угол между прямой КС и плоскостью квадрата равен 60. АВ=18см,.Найти угол между плоскостями АКС и ОКВ.
| |
| Основание пирамиды SАВСД - квадрат. Высота SО падает в центр вписанной в квадрат окружности. Построить линейные углы двугранных углов при рёбрах основания пирамиды.
| Через вершину квадрата ABCD проведен перпендикуляр DK = 10 см. Угол между плоскостями ABC и KBC равен 45º. Найти площадь квадрата.
| Стороны АС правильного треугольника АВС лежит в плоскости α. Угол между плоскостями треугольника 4α равен 60º; АС=12 см. Найти расстояние от точки в до плоскости α.
| |
| Основание пирамиды АВСД- прямоугольник АВСД; высота SА. Построить линейные углы двугранных углов при рёбрах АВ и АС
| Угол между плоскостями α и β равен 60º точка А, лежащая в плоскости α удалена от β на 12 см. Найти расстояние от точки А до линии пересечения.
| Через вершину D тупого угла ромба АВСD проведен перпендикуляр DM равный 9,6 см. Диагонали ромба равны 12 см и 16 см. Вычислить углы между плоскостями АВС и МВС
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Классификация холодных блюд и закусок. Урок №2 Тема: Холодные блюда и закуски. Значение холодных блюд и закусок. Классификация холодных блюд и закусок. Кулинарная обработка продуктов...
ТЕРМОДИНАМИКА БИОЛОГИЧЕСКИХ СИСТЕМ. 1. Особенности термодинамического метода изучения биологических систем. Основные понятия термодинамики. Термодинамикой называется раздел физики...
Травматическая окклюзия и ее клинические признаки При пародонтите и парадонтозе резистентность тканей пародонта падает...
|
Тема: Изучение приспособленности организмов к среде обитания Цель:выяснить механизм образования приспособлений к среде обитания и их относительный характер, сделать вывод о том, что приспособленность – результат действия естественного отбора...
Тема: Изучение фенотипов местных сортов растений Цель: расширить знания о задачах современной селекции. Оборудование:пакетики семян различных сортов томатов...
Тема: Составление цепи питания Цель: расширить знания о биотических факторах среды. Оборудование:гербарные растения...
|
|