Определение основных свойств функции
| |
|
|
|
|
| | | Найдите область определения функции y=f(x)
| Найдите значения аргумента при которых функция y=f(x) положительная
| Найдите значение функции у в точке x  , если , если
| Найдите
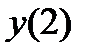 , ,  , , 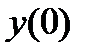 , ,  .
Постройте график данной функции.
Определите свойства функции по графику .
Постройте график данной функции.
Определите свойства функции по графику
| Найдите функцию, обратную данной. Укажите область определения и область значений обратной функции. Постройте графики данной функции и обратной в одной системе координат
| | *
| а) y= 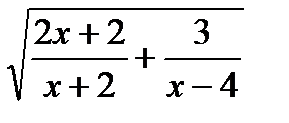 б)
б) 
| y=  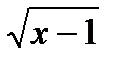
| y =  f(x)-чётная, g(x)-нечётная, f(x0)=5,g(x0)=1
f(x)-чётная, g(x)-нечётная, f(x0)=5,g(x0)=1
| 
| а)  б)
б)  , ,  в)
в) 
| |
| а) y=  б)
б) 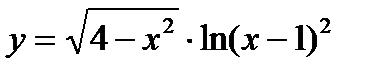
| y= 
| y =  f(x)-нечётная, g(x)-чётная, f(x0)=5,g(x0)=3
f(x)-нечётная, g(x)-чётная, f(x0)=5,g(x0)=3
| 
| а) 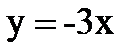 б)
б)  , ,  в)
в) 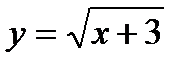
| |
| а) y=  б)
б) 
| y= 
| y =  f(x)-чётная, g(x)-чётная, f(x0)=0,g(x0)=1
f(x)-чётная, g(x)-чётная, f(x0)=0,g(x0)=1
| 
| а)  б)
б)  , ,  в)
в) 
| |
| а) y=  б)
б) 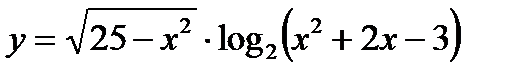
| y= 
| y =  f(x)-нечётная, g(x)-нечётная,f(x0)=2,g(x0)=4 f(x)-нечётная, g(x)-нечётная,f(x0)=2,g(x0)=4
| 
| а) 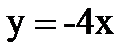 б)
б)  , ,  в)
в) 
| |
| а) y=  б)
б) 
| y= 
| y =  f(x)-чётная, g(x)-нечётная, f(x0)=1,g(x0)=2
f(x)-чётная, g(x)-нечётная, f(x0)=1,g(x0)=2
| 
| а)  + 1
б) + 1
б)  в)
в) 
|
| |
|
|
|
|
| |
| а) y=  
| y= 
| y =  f(x)-нечётная, g(x)-чётная, f(x0)=3,g(x0)=4 f(x)-нечётная, g(x)-чётная, f(x0)=3,g(x0)=4
| 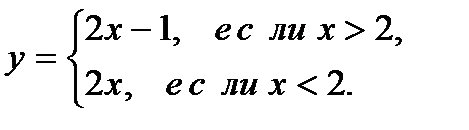
| а) 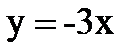 - 2
б) - 2
б)  в)
в) 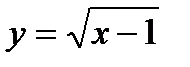
| |
| а) y=  б)
б) 
| y= 
| y = 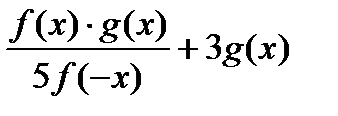 f(x)-чётная, g(x)-чётная, f(x0)=1,g(x0)=3
f(x)-чётная, g(x)-чётная, f(x0)=1,g(x0)=3
| 
| а)  + 3
б) + 3
б)  , ,  в)
в) 
| |
| а) y=  б)
б) 
| y= 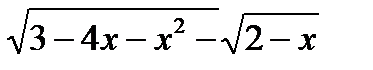
| y = 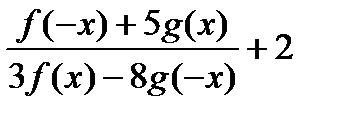 f(x)-нечётная, g(x)-нечётная,f(x0)=6,g(x0)=0 f(x)-нечётная, g(x)-нечётная,f(x0)=6,g(x0)=0
| 
| а) 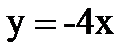 - 1
б) - 1
б) 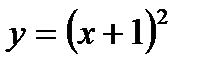 , ,  в)
в) 
| |
| а) y=  б)
б) 
| y= 
| y =  f(x)-чётная, g(x)-нечётная, f(x0)=2,g(x0)=3 f(x)-чётная, g(x)-нечётная, f(x0)=2,g(x0)=3
| 
| а) 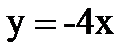 - 2
б) - 2
б)  , ,  в)
в) 
| |
| а) y=  б)
б) 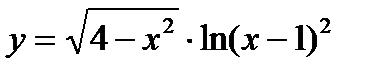
| y= 
| y =  f(x)-нечётная, g(x)-чётная, f(x0)=1,g(x0)=0 f(x)-нечётная, g(x)-чётная, f(x0)=1,g(x0)=0
| 
| а)  - 4
б) - 4
б)  в)
в) 
| |
| а) y=  б)
б) 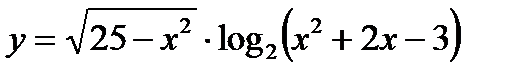
| y= 
| y =  f(x)-нечётная, g(x)-нечётная,f(x0)=0,g(x0)=2 f(x)-нечётная, g(x)-нечётная,f(x0)=0,g(x0)=2
| 
| а) 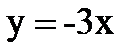 + 1
б) + 1
б)  , ,  в)
в) 
|
Простейшие преобразования графиков функций
| | I
| | | Дан график функции y = f (x).
Постройте графики следующих функций:
| 1y = f (x+1)
2y = f (x) +1
3y = f (x-2)
| 4y = f (x) – 2
5y = - f (x)
6y = f (-x)
| 7y = 2f (x)
8y = f (2x)
9y = f (x/3)
| 10y = 1- 3f (x)
11y = | g (x) |
12y = g (|x|)
|
| | *
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Вопрос. Отличие деятельности человека от поведения животных главные отличия деятельности человека от активности животных сводятся к следующему: 1...
Расчет концентрации титрованных растворов с помощью поправочного коэффициента При выполнении серийных анализов ГОСТ или ведомственная инструкция обычно предусматривают применение раствора заданной концентрации или заданного титра...
Психолого-педагогическая характеристика студенческой группы
Характеристика группы составляется по 407 группе очного отделения зооинженерного факультета, бакалавриата по направлению «Биология» РГАУ-МСХА имени К...
|
Что такое пропорции?
Это соотношение частей целого между собой. Что может являться частями в образе или в луке...
Растягивание костей и хрящей. Данные способы применимы в случае закрытых зон роста.
Врачи-хирурги выяснили...
ФАКТОРЫ, ВЛИЯЮЩИЕ НА ИЗНОС ДЕТАЛЕЙ, И МЕТОДЫ СНИЖЕНИИ СКОРОСТИ ИЗНАШИВАНИЯ Кроме названных причин разрушений и износов, знание которых можно использовать в системе технического обслуживания и ремонта машин для повышения их долговечности, немаловажное значение имеют знания о причинах разрушения деталей в результате старения...
|
|