Решение треугольников
| |
|
|
|
|
| | | Решите прямоугольный треугольник
| Решите прямоугольный треугольник
| Решите треугольник
| Решите треугольник
| Решите треугольник
| | *
| С=90о
А=34о12’
c=29,3
| C=90о
a=3,2
c=8,7
| b=3,29
a=5,78
C=111о7’
| b=49,7
A=34о51’
C=48о32’
| a=5,7
b=3,2
c=6,8
| |
| C=90о
B=64о39’
c=459
| a=984
b=321
C=90о
| b=34,9
c=91,3
A=34о7’
| c=0,284
C=121о47’
A=12о36’
| a=2,1
b=2,7
c=3,4
| |
| c=0,345
C=90о
A=49о15’
| a=2,1
b=9,1
C=90о
| B=17о25’
a=0,34
c=2,98
| a=34,9
A=19о54’
B=24о13’
| a=1,35
b=2,72
c=1,94
| |
| B=26о37’
C=90о
a=43,1
| a=984
b=321
C=90о
| a=0,284
c=1,315
B=97о34’
| a=4,7
B=19о39’
C=27о48’
| a=1,28
b=3,06
c=2,18
| |
| B=46о21’
C=90о
b=39,1
| a=94
b=31
C=90о
| b=34,12
c=17,47
A=51о59’
| b=49,7
A=34о51’
C=48о32’
| a=90,24
b=15,13
c=76,12
| |
| C=90о
A=13о58’
c=2,133
| a=0,934
b=2,317
C=90о
| b=3,219
a=5,784
C=111о7’
| a=34,9
A=109о54’
B=24о13”
| a=5,77
b=3,12
c=6,84
| |
| B=36о19’
C=90о
c=9,243
| a=2,13
b=9,19
C=90о
| B=17о19’
a=0,34
c=2,98
| a=34,9
A=109о54’
B=15о13’
| a=1,315
b=2,712
c=1,924
| |
| A=39о47’
C=90о
a=364
| b=24,39
c=81,13
C=90о
| b=34,9
c=91,3
A=34о7’
| c=3,24
B-141о12’
A=11о53’
| a=1,284
b=3,061
c=2,181
| |
| C=90о
B=64о39’
c=459
| C=90о
a=0,9
b=1,3
| B=17о1’
a=0,34
c=2,98
| b=49,7
A=34о51’
C=48о32’
| a=1,315
b=2,712
c=1,924
| |
| C=90о
B=64о39’
c=459
| C=90о
b=21,14
a=91,29
| B=7о19’
a=0,34
c=2,98
| c=3,24
B-14о12’
A=11о3’
| a=1,315
b=2,712
c=1,924
| |
| B=26о37’
C=90о
a=43,1
| С=90о
а=0,457
с=1,381
| B=25о19’
a=0,34
c=2,98
| a=34,9
A=109о54’
B=24о13’
| a=5,27
b=3,22
c=6,34
|
Преобразования тригонометрических выражений
| |
|
|
|
|
|
| | | По значению одной из тригонометрических функций найдите значения трёх остальных
| Упростите
| Вычислите
| Докажите тождество
| Определите, верно ли равенство
| Преобразуйте в произведение
| | *
| а) 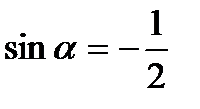 , ,  б) б)  
| 
| а) сos5850;б) tg 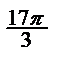
| 
| sin5cos7– sin10cos2=
-sin5cos3
| 
| |
| а)  , ,  б) б)  
| 
| а) sin91350;б)ctg 
| 
| cos4cos6 – sin1sin3=
cos7cos3
| 
| |
| а)  , ,  б) б) 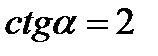 
| 
| а) tg13950;б) sin 
| 
| sin1sin3 - cos4cos6=
- cos7cos3
| 
| |
| а)  , ,  б) б)  
| 
| а) ctg6300;б)cos 
| 
| cos6cos4 – sin3sin1=
cos3cos7
| 
| |
| а) 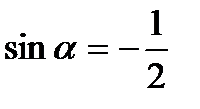 , ,  б) б)  
| 
| а) сos6750;б) tg 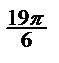
| 
| sin3sin1 – cos6cos4=
- cos7cos3
| 
| |
| а)  , ,  б) б)  
| 
| а) sin4950;б) ctg 
| 
| cos4cos6 - sin1sin3=
cos7cos3
| 
| |
| а)  , ,  б) б)  
| 
| а) tg7650;б) sin 
| 
| cos6cos4 – sin3sin1=
cos3cos7
| 
| |
| а)  , ,  б) б)  
| 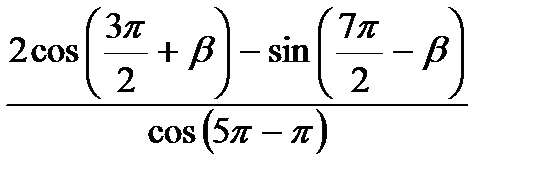
| а) ctg8100;б) cos 
| 
| sin1sin3 - cos4cos6=
- cos7cos3
| 
| |
| а) 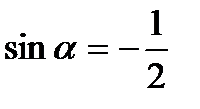 , ,  б) б) 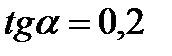 
| 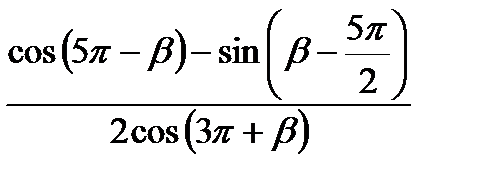
| а) сos9000;б) tg 
| 
| sin3sin1 – cos6cos4=
- cos7cos3
| 
| |
| а)  , ,  б) б)  
| 
| а) sin3950;б) ctg 
| 
| sin5cos7-sin10cos2=
- sin5cos3
| 
| |
| а) 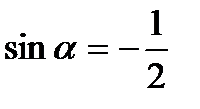 , ,  б) б) 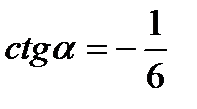 
| 
| а) сos5750;б)cos 
| 
| sin3sin1 – cos6cos4=
- cos7cos3
| 
|
Решение тригонометрических уравнений
| |
|
|
|
|
|
| |
| Решите уравнение
| Решите уравнение
| Решите уравнение
| Решите уравнение
| Решите уравнение
| Решите уравнение
| | *
| 
| 
| 
| 
| 
| 
| |
| 
| 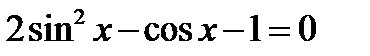
| 
| 
| 
| 
| |
| 
| 
| 
| 
| 
| 
| |
| 
| 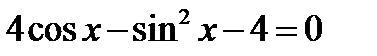
| 
| 
| 
| 
| |
| 
| 
| 
| 
| 
| 
| |
| 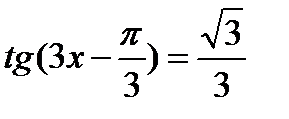
| 
| 
| 
| 
| 
| |
| 
| 
| 
| 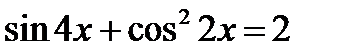
| 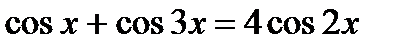
| 
| |
| 
| 
| 
| 
| 
| 
| |
| 
| 
| 
| 
| 
| 
| |
| 
| 
| 
| 
| 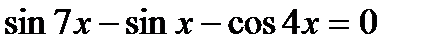
| 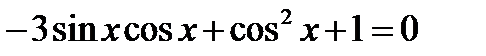
| |
| 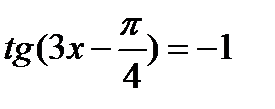
| 
| 
| 
| 
| 
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
Гносеологический оптимизм, скептицизм, агностицизм.разновидности агностицизма Позицию Агностицизм защищает и критический реализм. Один из главных представителей этого направления...
Функциональные обязанности медсестры отделения реанимации · Медсестра отделения реанимации обязана осуществлять лечебно-профилактический и гигиенический уход за пациентами...
|
Этапы трансляции и их характеристика Трансляция (от лат. translatio — перевод) — процесс синтеза белка из аминокислот на матрице информационной (матричной) РНК (иРНК...
Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни...
Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана...
|
|