Уравнение сохранения энергии
В общем случае закон сохранения энергии (первый закон термодинамики) можно сформулировать следующим образом: изменение энергии термодинамического тела (газа) равно сумме работы, совершенной средой над телом (dlвн) и количества теплоты (dqвн), подведенного к телу со стороны окружающей среды за некоторый промежуток времени. Для 1 кг газа уравнение 1-го закона термодинамики в дифференциальной форме de = dlвн + dqвн. (2.7) Подводимые к газу работа и теплота считаются положительными, а отводимые – отрицательными. Тогда для компрессорных машин: dlвн >0, dqвн <0. Для потока газа изменение энергии газа складывается из изменения кинетической энергии (
Для компрессорных машин работа, совершаемая против сил тяжести незначительна и можно принять dhz ≈ 0. Для потока газа, двигающегося по каналу между сечениями 1-1 и 2-2
Рис. 2.1. К первому закону термодинамики для потока газа
Таким образом, для перемещения порции газа между двумя сечениями со стороны внешней среды подводится так называемая работа проталкивания
или в дифференциальной форме
Кроме того, если к газу подводится работа от лопаток рабочего колеса, называемая в термодинамике технической (в теории турбокомпрессоров ее называют внутренней dli), то внешняя работа будет определяться как
Подставим выражение (2.8) и (2.9) в (2.7)
Из термодинамики известно, что приращение энтальпии массы газа
Подставляя (2.11) в (2.10), получим уравнение закона сохранения энергии в дифференциальной форме
Проинтегрируем уравнение (2.12) между сечениями 1-1 и 2-2 канала с учетом принятых знаков для dli и dqвн (в случае отвода теплоты в процессе сжатия)
Если в процессе сжатия в компрессоре тепло от газа не отводится (неохлаждаемые компрессоры), то, интегрируя уравнение (2.12) можно записать
Из этого уравнения видно, что внешние теплота и работа, подводимые к 1 кг газа идут на изменение энтальпии и кинетической энергии. При li =0 и qвн =0 в уравнении (2.14) полная энергия потока остается постоянной:
Полными или заторможенными параметрами (i *, P *, T *) будет обладать газовый поток, если его представить неподвижным (заторможенным), но с энергией, равной энергии потока. Полные параметры имел бы газ, если бы его кинетическая энергия без теплообмена и потерь перешла бы во внутреннюю энергию. Такой процесс торможения соответствует адиабатному процессу. Из условия постоянства полной энтальпии для совершенного газа можно записать выражение для полной температуры
Из условия адиабатного процесса торможения можно определить полное давление
Путем разложения в ряд выражения (2.17) можно получить формулу, справедливую при скоростях, достаточно удаленных от звуковой скорости
|

 ), внутренней энергии (dU = cvdT), потенциальной энергии в поле сил тяжести земли dhz = gdz, тогда
), внутренней энергии (dU = cvdT), потенциальной энергии в поле сил тяжести земли dhz = gdz, тогда . (2.8)
. (2.8)
 ,
,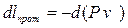 .
. . (2.9)
. (2.9) , или
, или . (2.10)
. (2.10) . (2.11)
. (2.11) . (2.12)
. (2.12) , или
, или . (2.13)
. (2.13) . (2.14)
. (2.14) . (2.15)
. (2.15) . (2.16)
. (2.16) . (2.17)
. (2.17) . (2.18)
. (2.18)


