Уравнение Бернулли
Уравнение Бернулли можно рассматривать как одну из форм уравнения сохранения энергии. Его можно получить, используя уравнение сохранения энергии в абсолютном движении (2.12) и уравнение первого закона термодинамики:
где dq – приращение полного количества теплоты, воспринимаемого газом. Подставив уравнение 1-го закона термодинамики в выражение (2.11), получим
используя правило Лагранжа
Заменив приращение энтальпии в уравнении (2.12) формулой (2.20)
Полагая, что разность полного количества теплоты подведенного к газу и внешнего теплообмена дает количество теплоты, выделяющееся в процессе трения
получим уравнение Бернулли
пользуясь тем, что теплота трения эквивалентна затратам работы на преодоление трения (
В интегральной форме уравнение Бернулли (2.21) для процесса сжатия в турбокомпрессоре:
Из уравнения (2.22) следует, что в турбокомпрессоре работа, подведенная к газу от рабочего колеса, идет на работу сжатия и перемещения газа, увеличение кинетической энергии и преодоление сил трения. Применительно к процессам сжатия в турбокомпрессорах понятие удельной работы, т.е. работы, отнесенной к 1 кг газа, заменяют понятием напора. То есть напором называется энергия, подведенная к одному килограмму газа (h, кДж/кг). В уравнении Бернулли удельная работа сжатия и перемещения газа (эффективная или полезная работа) называется полезным или статическим напором и в зависимости от характера процесса может именоваться политропным, адиабатным или изотермным напором
Удельная кинетическая энергия соответствует динамическому напору
Затраты работы на преодоление сил трения соответствуют потерям напора на трение Техническая (или внутренняя) работа, затраченная на вращение рабочего колеса, соответствует внутреннему напору В итоге уравнение Бернулли в интегральной форме через напоры:
Сумму статического и динамического напоров называют полезным напором по полным параметрам
|

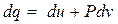 , (2.19)
, (2.19)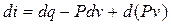 ,
,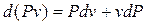 , запишем
, запишем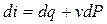 . (2.20)
. (2.20)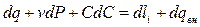 , или
, или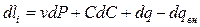 ,
,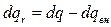 ,
,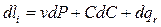 ,
,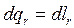 ), произведем замену
), произведем замену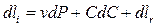 . (2.21)
. (2.21)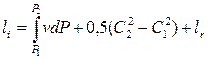 . (2.22)
. (2.22)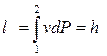 .
.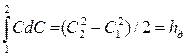 .
. .
. .
.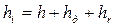 . (2.23)
. (2.23)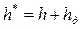 .
.


