Основные уравнения механики жидкости и газа
На частицу газа в потоке действуют поверхностные, массовые силы и силы инерции. К поверхностным относятся силы давления и силы трения, к массовым – сила тяжести, силы магнитного и электрического взаимодействия.
1. Уравнение движения Согласно принципу Даламбера, сила инерции равна и противоположно направлена сумме всех сил, действующих на частицу газа:
где В механике сплошных сред сила инерции, отнесенная к единице массы частицы газа, Н/кг:
При течении газа в проточной части турбокомпрессора массовые силы (сила тяжести) незначительны по сравнению с силами трения
Сила давления
где Сила трения представляет собой дивергенцию тензора скоростей деформации
где Из уравнений (3.3), (3.6) и (3.7) можно получить основное уравнение движение вязкого газа – уравнение Навье-Стокса. Запишем его в проекциях на оси координат, используя форму математической записи через оператор Гамильтона [3]:
где Стоящие в левой части уравнения (3.8) силы инерции в проекциях на оси координат расписываются через частные производные
Для идеального газа (без учета вязкости) уравнения Навье-Стокса (3.8) преобразуются к уравнениям Эйлера:
В проекциях на оси:
Неизвестными в уравнениях Навье-Стокса и Эйлера являются 5 величин: проекции абсолютной скорости Cr, Cu, Cz, давление Р и плотность ρ;.
2. Уравнение неразрывности (сохранения массового расхода):
где В случае стационарного потока
В случае одномерного потока для струйки тока
Для ступени турбокомпрессора
3. Уравнение энергии:
4. Уравнение состояния: – идеального газа
– реального газа
Система уравнений (3.8), (3.11), (3.12), (3.13) включает в себя 6 уравнений с шестью неизвестными. Кроме Сr, Cu, Cz, P, ρ;, уравнение состояния вносит шестую неизвестную – температуру Т. Если учитывать теплообмен с окружающей средой, то появляется седьмое неизвестное – количество подведенной (отведенной) теплоты qвн. Дополнительный уравнением будет условие теплообмена с окружающей средой, описываемое уравнением Ньютона:
где α; – коэффициент теплоотдачи, Вт/(м2·К); Токр – температура окружающей среды, К; F – площадь поверхности теплообмена, м2. Таким образом, система уравнений получается замкнутой. И сформулировав граничные (а в случае нестационарного движения и начальные) условия теоретически эта система может быть решена. Однако в настоящее время отсутствует возможность интегрирования уравнений Навье-Стокса, Эйлера и Рейнольдса [3] в полной форме. На практике идут на различные упрощения: считают процесс стационарным, переходят к двух и одномерным моделям течения, не учитывают вязкость. Обоснованность этих допущений должна быть оговорена для каждой конкретной задачи и опираться на опытные данные.
|

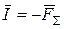 , (3.3)
, (3.3)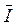 – сила инерции;
– сила инерции; 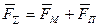 – сумма внешних сил (массовых
– сумма внешних сил (массовых 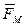 и поверхностных
и поверхностных 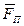 ).
).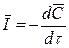 . (3.4)
. (3.4)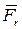 и силами давления
и силами давления 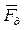
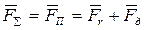 . (3.5)
. (3.5)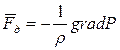 , (3.6)
, (3.6)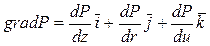 – градиент давления (
– градиент давления (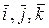 – единичные векторы положительных направлений осей z, r, u.
– единичные векторы положительных направлений осей z, r, u.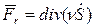 , (3.7)
, (3.7)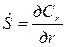 – для оси r;
– для оси r; 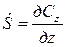 – для оси z;
– для оси z; 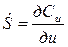 – для оси u;
– для оси u; 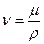 – коэффициент кинематической вязкости, м2/с; μ; – коэффициент динамической вязкости, Па·с.
– коэффициент кинематической вязкости, м2/с; μ; – коэффициент динамической вязкости, Па·с.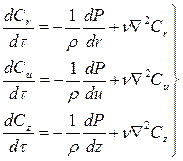 , (3.8)
, (3.8)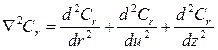 (
(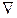 – оператор Гамильтона, D=
– оператор Гамильтона, D= 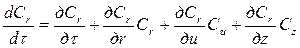 ,
,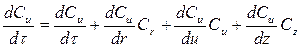 ,
,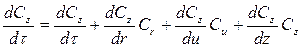 .
.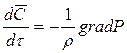 . (3.9)
. (3.9)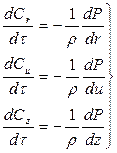 . (3.10)
. (3.10)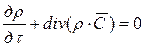 , (3.11)
, (3.11)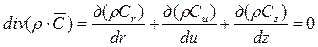
 , тогда
, тогда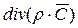 =0.
=0.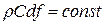 .
.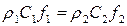 .
.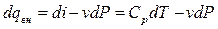 . (3.12)
. (3.12)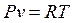 ; (3.13)
; (3.13)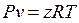 .
.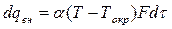 , (3.14)
, (3.14)


