Преобразование уравнений движения методами теории подобия
В большинстве важных практических случаев применение уравнений Навье-Стокса и Эйлера возможно путем преобразования этих уравнений методами теории подобия. Напомним основные понятия и определения теории подобия, известные из дисциплины «Механика жидкости и газа». Теория подобия – учение о методах научного обобщения эксперимента. Применение теории подобия позволяет вместо дорогостоящих опытов на промышленной аппаратуре выполнять исследования на моделях значительно меньшего размера. Подобными называют явления, для которых постоянны отношения характеризующих их сходственных величин. Константами подобия называются безразмерные масштабные множители, выражающие отношения однородных сходственных величин подобных систем. Инвариантами подобия называются безразмерные отношения каких-либо двух размеров одной системы, равные отношению сходственных размеров подобной системы. Например: a, b, l – размеры модели; A, B, L – размеры натуры;
Константы и инварианты подобия, полученные отношением линейных размеров, являются условиями геометрического подобия. Другими словами, геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров натуры и модели. Инварианты подобия не обязательно могут быть выражены отношением линейных размеров модели и натуры. В них могут фигурировать любые физические величины процессов, протекающих в модели и натуре. Инварианты подобия, выраженные отношениями двух однородных физических величин, называются симплексами. Инварианты подобия, выраженные отношениями разнородных физических величин, представляют собой безразмерные комплексы. Динамическим подобием называют условия подобия сил, действующих на сходственные частицы в натуре и модели. Динамическое подобие обеспечивается равенством безразмерных комплексов в модели и натуре. Кинематическим подобием называют условие подобия траектории движения сходственных частиц в натуре и модели. Основные положения теории подобия обобщаются теоремами подобия. 1-я теорема подобия (теорема Ньютона): При подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы. 2-я теорема подобия (теорема Бэкингема): Решение любого дифференциального уравнения может быть представлено в виде зависимости между безразмерными комплексами этих величин, то есть между критериями подобия. 3-я теорема подобия (Кирпичев): Подобны те явления, определяющие критерии которых численно равны. Теория подобия позволяет преобразовать уравнения Навье–Стокса и получить из них некоторую общую функциональную зависимость между критериями подобия, характеризующими силы, действующие при движении вязкого газа или жидкости. Запишем уравнение Навье–Стокса для оси z (с учетом массовых сил – сил тяжести)
Критерии подобия можно получить путем деления левой части дифференциального уравнения на правую (или наоборот) и последующего отбрасывания знаков математических операторов. Если поток стационарный, то Если течение одномерное, то
Отбрасывая знаки дифференциалов и заменяя текущую координату z на некоторый определяющий линейный размер l, получим
Разделим правую часть уравнения на левую, которая представляет собой силу инерции
В правой части мы получили выражения, характеризующие соотношения между соответствующими силами и силой инерции, то есть за масштаб принята сила инерции. Комплекс
Критерий Фруда представляет собой меру отношения сил инерции к силе тяжести в подобных потоках. Комплекс
Критерий Эйлера представляет собой отношение изменения силы гидростатического давления к силе инерции в подобных потоках. Комплекс величин
Критерий Рейнольдса представляет собой отношение силы трения к силе инерции в подобных потоках. При неустановившемся движении
получаем критерий гомохронности (Но) или критерий Струхала (Sh)
Критерий Струхала учитывает неустановившийся характер движения в подобных потоках. В турбокомпрессорах вместо критерия Эйлера обычно пользуются двумя другими безразмерными параметрами – числом Маха (
Следовательно, число Маха и показатель изоэнтропы также могут считаться критериями динамического подобия. Если какой-либо параметр не влияет на протекание процесса, то процесс называют автомодельным по отношению к этому параметру.
|

 – константа геометрического подобия;
– константа геометрического подобия; – инвариант геометрического подобия.
– инвариант геометрического подобия. .
. .
. .
. .
.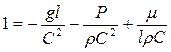 .
. называется критерием Фруда. Чтобы избежать чисел < 1, пользуются обратным выражением
называется критерием Фруда. Чтобы избежать чисел < 1, пользуются обратным выражением .
. называется критерием Эйлера. Обычно вместо давления Р используется перепад давлений DР:
называется критерием Эйлера. Обычно вместо давления Р используется перепад давлений DР: .
.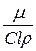 называется критерием Рейнольдса. Чтобы избежать чисел меньше 1, используют обратное отношение:
называется критерием Рейнольдса. Чтобы избежать чисел меньше 1, используют обратное отношение: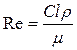 .
.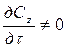 . Заменив член, отражающий влияние нестационарности движения
. Заменив член, отражающий влияние нестационарности движения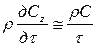 ,
, .
. ) и показателем изоэнтропы
) и показателем изоэнтропы  . Они связаны между собой. Если вместо перепада давлений Δ Р взять абсолютное давление Р и заменив
. Они связаны между собой. Если вместо перепада давлений Δ Р взять абсолютное давление Р и заменив 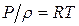 , получим
, получим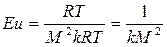 .
.


