ОБЩИЕ ПОЛОЖЕНИЯ. Окончательное поражение хазарам нанес киевский князь Святослав
Окончательное поражение хазарам нанес киевский князь Святослав. В 965 году он разгромил хазарские войска, взял Саркел и победил ясов и касогов. В 968 - 969 гг. его дружины разрушили Итиль и Семендер. В 985 г. киевский князь Владимир в союзе с гузами воевал в Волжской Булгарии, а затем, спустившись по Волге, овладел Хазарией и наложил на нее дань. Хазарская держава перестала существовать. Однако хазары не исчезли окончательно. Отдельные их группы упоминаются в хрониках последующих столетий, в частности, в Тмутаракани проживала многочисленная хазарская община.
Рег. № М-624 МАТЕМАТИКА
Методические указания к изучению дисциплины и выполнению контрольной работы № 3 для студентов заочной формы обучения
Для всех специальностей
Санкт-Петербург Допущено редакционно-издательским советом СПбГИЭУ в качестве методического издания
Составители: ст. преп. В.Г. Блинова канд. техн. наук, доц. Я В. Войтишек ст. преп. Е.Н. Зверева
Рецензент канд. хим. наук, доц. В.В. Фокин
Подготовлено на кафедре высшей математики
Одобрено научно-методическим советом университета
Отпечатано в авторской редакции с оригинал-макета, представленного составителями © СПбГИЭУ, 2009 Содержание 1. Общие положения……………………………………………...4 2. Методические указания к изучению дисциплины.…………..4 3. Методические указания к выполнению заданий № 1- № 4 Комментарии к задаче № 1 §1. Случайные события. Основные понятия…………………….5 §2. Случайные события. Операции………………………………6 §3. Классическое определение вероятности……………………..6 §4. Примеры задач на классическую вероятностную схему……8 §5. О статистической и геометрической вероятностях…………9 §6. Простейшие свойства вероятностей………………………..10 §7. Условные вероятности. Независимость событий………….11 §8. Вероятность наступления хотя бы одного события……….12 §9. Формула полной вероятности………………………………14 §10. Формула Байеса……………………………………………..16 Комментарии к задаче № 2 §11. Повторные независимые испытания………………………17 §12. Другие формулы вычисления вероятностей для схемы Бернулли………………………………………………………………19 Комментарии к задаче № 3 §13. Случайные величины дискретного типа…………………..22 §14. Функция распределения…………………………………….23 §15. Математическое ожидание случайной величины дискретного типа…………………………………………………24 §16. Дисперсия случайной величины…………………………..26 §17. Биномиальный и пуассоновский законы распределения…26 Комментарии к задаче № 4 §18. Случайные величины непрерывного типа…………………28 §19. Нормальный закон распределения и его характеристики…………………………………………………………………..30 §20. Другие законы распределения непрерывных случайных величин………………………………………………………………31 4. Методические указания к выполнению задания № 5……….32 5. Контрольные задания № 1- № 4.……………………………...53 6. Контрольные задания № 5.……………………………………71 7. Выбор варианта. Требования к оформлению контрольной работы.……………………………………………………..…..79 8. Список литературы……………………………………….…...80 Приложение 1 Таблица случайных чисел…………….………...81 Приложение 2 Нормированная функция Лапласа.………….………83 Приложение 3 Значения чисел q в зависимости от объёма выборки n и надёжности Приложение 4 Критические точки распределения Приложение 5 Содержание дисциплины..………………….…..87 Приложение 6 Образец оформления титульного листа контрольной работы.………………………………………………....90 Приложение 7 Перечень контрольных вопросов для проверки знаний по дисциплине.……………………………….91 ОБЩИЕ ПОЛОЖЕНИЯ Цель дисциплины «Математика (Теория вероятностей и математическая статистика)» - дать необходимый математический аппарат и привить навыки его использования при решении инженерно-экономических задач. Для этого при изучении курса студенты осваивают методы математического моделирования экономических и иных возникающих на практике ситуаций, вероятностные методы их исследования и решения, методы обработки статистических данных (аналитически и при помощи вычислительной техники), а также методы дальнейшего анализа полученных результатов. Это способствует также развитию логического и алгоритмического мышления. Теория вероятностей опирается на предшествующие разделы математики, как на курс средней школы, так и на разделы, изучавшиеся на 1 курсе (множества, функции, непрерывность, производные, интегралы, ряды). Студенты 2 курса, имеющие зачтенные контрольные работы № 3 и № 4, допускаются к экзамену по математике.
|


 для определения доверительного интервала среднего квадратического отклонения
для определения доверительного интервала среднего квадратического отклонения 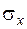 .….………………….85
.….………………….85 ...…….…86
...…….…86


