Типовой пример
Получены статистические данные (N=500) зависимости результатов измерения роста студентов (Х) от окружности груди (Y). Измерения проводились с точностью до 1 см.
Таблица 1 Статистические данные типового примера
…………..
Требуется: 1 часть. 1) произвести выборку из 200 значений; 2) построить эмпирическую функцию распределения, полигон, гистограмму для случайной величины Х; 3) построить точечные и интервальные оценки для мат. ожидания и дисперсии генеральной совокупности Х; 4) сделать статистическую проверку гипотезы о законе распределения случайной величины Х; часть 2. 1) нанести на координатную плоскость данные выборки (x;y) и по виду корреляционного облака подобрать вид функции регрессии; 2) составить корреляционную таблицу по сгруппированным данным; 3) вычислить коэффициент корреляции; 4) получить уравнение регрессии;
Решение. 1) Произведём из генеральной совокупности N =500 выборку n =200 значений. Для этого воспользуемся таблицей случайных чисел (Приложение А). Выберите столбец, номер которого соответствует месяцу Вашего рождения. В этом столбце отсчитайте порядковый номер даты дня рождения. В полученном случайном числе определите номера ещё трёх столбцов. Для данного примера выбрана дата 31 декабря. В 12 столбце определили 31 номер случайного числа. Это число 0436. Значит выбранными будут столбцы №12;4;13;16. (№12 – месяц Вашего рождения, №4 – первая или вторая цифра в случайном числе, которая не использовалась, №13 – третья цифра в случайном числе +10, №16 – четвёртая цифра в случайном числе +10). Если цифры повторяются, то нужно взять со3седние номера. Например, случайное число во втором столбце - 4422. Нужно выбрать номера 2,4,12,13. Для осуществления выборки берутся последние три цифры в случайном числе, которые определяют порядковый номер выборочного значения. Если в выборке встретился номер, которого нет в генеральной совокупности, то необходимо вычислить разность между этим числом и 500. Если полученный номер уже выбрали, то необходимо выбрать следующий за ним номер. Для представленного примера получилась выборка:
Таблица 2 Выборочные данные X и Y
Продолжение таблицы 2
Составим ранжированный (по увеличению) ряд для случайной величины Х. Таблица 3 Ранжированный ряд случайной величины Х
Окончание таблицы 3
Cоставим новую таблицу, в которой отразим частоты появления случайных величин Таблица 4
|

 и относительные частоты
и относительные частоты 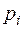 .
.


