Дискретный вариационный ряд.
В данном примере случайные величины сплошь заполняют промежуток (148;190). Число возможных значений велико. Их нельзя представить в виде случайных величин, принимающих отдельные, изолированные значения, тем самым отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Поэтому для построения вариационного ряда будем использовать интервальный ряд распределения. Весь возможный интервал варьирования разобьём на конечное число интервалов и подсчитаем частоту попадания значений величины в каждый интервал. Минимальное и максимальное значения случайной величины:
При этом значение признака, находящегося на границе интервалов относят к правой границе интервала. На практике считают, что правильно составленный ряд распределения содержит от 6 до 15 частичных интервалов. Часто интервальный вариационный ряд заменяют дискретным вариационным рядом, выбирая средние значения интервала (таблица №7). Для данного примера Таблица 5
|
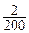
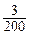
Тогда интервал варьирования R («размах») будет равен R= 
Длину интервала рассчитывают по формуле:
(6)
, округлим до 3, т.е. размер интервала h =3, а число интервалов будет равно 14. Соответствующий интервальный вариационный ряд приведён в таблице №5.
