ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
Пусть проводится n последовательных испытаний. Предположим, что эти испытания независимые, т.е. вероятность осуществления очередного исхода не зависит от реализации исходов предыдущих испытаний. Рассмотрим простейший случай, когда различных исходов всего два (“успех” и “неуспех”). Более того, речь пойдет о случае, когда вероятность “успеха” в каждом из испытаний неизменна и равна p, т.е. вероятность “неуспеха” также неизменна и равна q = 1 - p. Такие испытания называются испытаниями Бернулли. Простейшими примерами здесь могут служить: последовательное бросание монеты (с вероятностью “успеха” - выпадения “орла” - равной 0,5); последовательная стрельба по мишени с постоянной вероятностью “успеха” - попадания - в каждом выстреле; извлечение из урны, содержащей шары двух цветов, по одному шару с возвращением (и перемешиванием); и т. д. Я. Бернулли вычислил вероятность того, что в n последовательных “испытаниях Бернулли” произойдет ровно k “успехов”
(о вычислении числа
Пример 1. Вероятность того, что при 4 бросках игральной кости выпадут ровно 2 “четверки”, равна
Здесь p - вероятность выпадения “четверки” в одном броске - равна 1/6, q = 5/6, общее число испытаний n = 4, число “успехов” k = 2.
Пример 2. Вероятность попадания в мишень при одном выстреле p = 0,6. Какова вероятность, что при пяти выстрелах будет 3 попадания? Здесь n = 5, k = 3, q = 1 - p = 0,4,
Пример 3. В урне 4 белых и 2 черных шара. 6 раз извлекают по 1 шару, записывают цвет, а шар возвращают в урну и перемешивают шары. Какова вероятность, что среди записанных шаров более 4 белых? Пусть “успех” состоит в том, что вынут белый шар. Тогда p= 4/6 = 2/3 (из 6 шаров 4 белых), q = 1 - p = 1/3. По условию n= 6, k = 5 или k = 6, откуда искомая вероятность
Пример 4. Вероятность попадания в мишень при одном выстреле p = 0,6. Какова вероятность, что третье попадание произойдет в пятом выстреле? Эта задача отличается от рассмотренной в примере 2: там третье попадание может произойти и раньше пятого выстрела. Искомое событие является произведением двух следующих (независимых): А = {в первых 4 выстрелах ровно 2 попадания} и В={в пятом выстреле попадание}. P(A) вычисляется по формуле Бернулли
a P(B) = p = 0,6. Поэтому искомая вероятность равна
В общем случае вероятность того, что к-й “успех” произойдет ровно в n-м испытании Бернулли, равна
Пример 5. Вероятность попадания в мишень при одном выстреле p = 0,6. Какова вероятность, что в 5 выстрелах произойдет хотя бы 2 попадания? Мы знаем, что Р5(0) + Р5(1) + Р5(2) + Р5(3) + Р5(4) + Р5(5) = 1. В данной задаче нас интересует сумма четырех последних слагаемых: Заметим, что проще воспользоваться вероятностью противоположного события:1- P5(0)-P5(1)=1-0,45-5 0,44 0,6 = 0,91296.
§12. ДРУГИЕ ФОРМУЛЫ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ СХЕМЫ БЕРНУЛЛИ
Хотя формула Бернулли и является точной, она не всегда удобна. Например, при 100 бросках монеты
и вычисление точного ответа затруднительно. Формула Бернулли приемлема для вычислений, если число испытаний не превышает 10-15. При больших n используют либо формулу Лапласа, либо формулу Пуассона. Формула Лапласа (локальная теорема Лапласа)
тем точнее, чем больше n. Здесь n, k, p, q - те же величины, что и в формуле Бернулли. Функция j(x) четная: j(-x) = j(x). Она быстро убывает: считают, что при x > 4 j(x) = 0. Таблица, позволяющая вычислять значения функции j(x), имеется во всех учебниках и задачниках по теории вероятностей. Впрочем, можно не иметь таблицы, а иметь калькулятор, вычисляющий экспоненту (функцию ех).
Пример 1. Вероятность выпадения ровно 50 “орлов” при 100 бросках монеты Р100(50) вычислим по формуле Лапласа. Здесь n = 100,k = 50,p=0,5, q = 0,5, k - np = 0,
Пример 2. Найти вероятность выпадения от 47 до 57 “орлов” при 100 бросках монеты. При решении подобных задач (при n > 15) используют интегральную теорему Лапласа: вероятность Рn(k1,k2) появления события в n испытаниях от k1 до k2 раз
Здесь n, p, q те же, что и в примере 1: n=100, p = q =0,5, k1=47, k2 = 57.
Функция F вычисляется с помощью таблиц (см. приложение).
Функция Ф(x) нечетная: Ф(-х) = - Ф(х). При х > 5 считают, что Ф(х) = 0,5. Итак, Р100(47,57) = Ф(1,4) + Ф(0,6). По таблице Ф(1,4) = 0,4192, Ф(0,6) = 0,2257, поэтому Р100(47,57) = 0,6449. При небольших значениях вероятности p (меньших 0,1) и больших значениях n более точный результат дает другая приближенная формула - формула Пуассона
l называется параметром распределения Пуассона, а сама формула выражает “закон редких явлений” (т. к. p мало). Пример 3. Первый черновой набор “Методических указаний” на 50 страницах содержит 100 опечаток. Какое из событий вероятнее: на наудачу взятой странице нет опечаток, 1 опечатка, 2 опечатки, 3 опечатки? Вероятность того, что данная опечатка попадет на наудачу взятую страницу равна 1/50 = 0,02, число испытаний (опечаток) n = 100. Поскольку p мало, воспользуемся формулой Пуассона с параметром l = np = 2. Вероятность того, что опечаток нет
Другие вероятности
Как видим, наибольший коэффициент при е-2 у Р100(1) и Р100(2). Ответ: наиболее вероятны 1 или 2 опечатки, их вероятность
|


 см. §4).
см. §4).
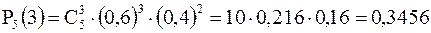 .
. .
. ,
,
 .
.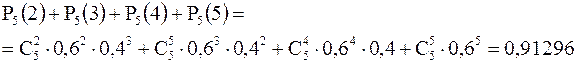
 ,
, ,
,  ,
, 
 и
и .
.


 , l = np
, l = np (т.к. 0! = 1)
(т.к. 0! = 1) ,
, 
 .
. .
.


