Нечеткая логика.

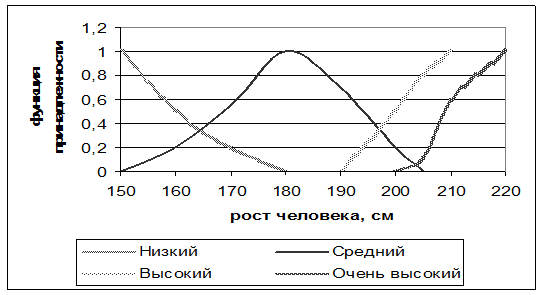
Другим приемом, позволяющим формализовать качественные характеристики решения, является использование аппарата нечетких множеств.

Здесь для каждого словесного значения вводится понятие нечеткая переменная. Нечеткая переменная: (наименование, количественная шкала, функция принадлежности), т. е. нечеткая переменная состоит из трех элементов: наименования характеристики, количественной шкалы, с помощью которой ее можно измерить, и дополнительной функции — так называемой функции принадлежности к данной характеристике.

Так как любая качественная, словесная характеристика содержит большую степень количественной неопределенности, то для раскрытия этой неопределенности вводится функция принадлежности, позволяющая строго оценить конкретную характеристику.

Например, нечеткие переменные: «низкий», «средний», «высокий» и «очень высокий» человек, которые в свою очередь являются значениями лингвистической характеристики «рост человека», графически могут быть представлены так.

Функция принадлежности с помощью чисел от 0 до1 отражает степень принадлежности словесной оценки к качественной характеристике, например для словесной оценки «высокий» функция принадлежности будет выражаться набором своих значений: (190/0; 200/0,5; 205/0,8; 210/1; 220/1), а для словесной оценки «очень высокий» набором (200/0; 205/0,1; 210/0,6; 220/1).

В этих выражениях на первом месте стоит значение количественной шкалы, в данном случае «рост в см», и через знак «/» стоит значение функции принадлежности.

Смысл значений функции принадлежности состоит в том, что чем ближе значение к 1, тем в большей степени значение соответствующей количественной шкалы принадлежит к наименованию нечеткой характеристики. В соответствии с данным графиком средний рост человека равен 180 см, так как на построенном графике функция принадлежности для этого значения количественной шкалы равна 1.

Человек с ростом 170 см согласно графику будет принадлежать уже к характеристике «средний» только со степенью 0,55, а человек с ростом 190 см — к характеристике «средний» со степенью 0,7.

Отметим, что функция принадлежности может быть построена ЛПР, рассчитана на основе некоторой дополнительной информации или определена экспериментально.

Конечно, функция принадлежности, построенная, например, ЛПР, будет содержать определенную долю субъективности, но, будучи построенной, она уже однозначно определяет, уточняет и позволяет измерять степень принадлежности к нечеткой характеристике.

Подчеркнем, что процесс формализации качественных словесных переменных связан с возможностью задать определенную количественную шкалу, по которой можно определить качественную характеристику.

В рассмотренном примере характеристики «рост человека» такой шкалой служил рост человека в см. Если же у рассматриваемой качественной характеристики нет подобной естественной шкалы, то в качестве количественной шкалы практически всегда можно взять шкалу баллов, например в 5,10,100 баллов.

Таким образом, понятие нечеткой переменной позволяет формализовать словесные характеристики решения.