Рассмотрим правило взвешенного произведения.
Вариант решения по данному правилу называется оптимальным, если среди всех имеющихся вариантов он обеспечивает максимум произведения коэффициентов приоритета характеристик аi, на логические функции требований μ(хi), т. е. обеспечивает
В этом выражении буквой П для сокращения записи обозначается произведение логических функций μ(x i) в степени аi. Такая форма критерия оптимальности обладает важной особенностью: если одна из величин μаi(хi) мала или равна нулю, то величина всего критерия также мала или равна нулю. Заметим, что при использовании критерия взвешенной суммы вклад каждой характеристики в общую сумму только увеличивает ее значение. Поэтому при использовании критерия взвешенного произведения говорят о его жесткости, так как он бракует любой вариант решения, который недостаточно удовлетворяет требованиям, предъявляемым ЛПР, хотя бы по одной характеристике решения. Это свойство критерия взвешенной суммы формулируется в виде аксиомы выбора оптимальных решений: если значение какой-либо характеристики сравниваемого варианта решения не удовлетворяет требованиям задания, то и значение критерия Например, если значение какой-либо из μ(xi) будет меньше 0,5, т. е. хуже среднего значения соответствующей характеристики хi, то значение критерия взвешенного произведения тоже будет меньше 0,5. Это простое для расчетов правило обеспечивает однозначный выбор при монотонных величинах логических функций и довольно широко применяется на практике.
|
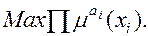
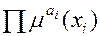тоже будет неудовлетворительным.
