Равноточных измерений
d1 = x1 - x1¢ d2 = x2 - x2¢ (24) ......... dn = xn - xn¢ Значения diявляются истинными погрешностями разностей двойных измерений, поэтому, используя формулу Гаусса (2), получим md = где n – число всех разностей. Средняя квадратическая погрешность одного измерения mxi = За окончательное, более надежное значение принимают
При mxi = mxi¢имеем
Формулы (26) – (28) применяют, когда ряд двойных измерений не имеет систематических ошибок. Если результаты измерений содержат систематические ошибки, то в значениях разностей diони значительно ослабляются и в di войдут остаточные систематические ошибки. Учитывая свойство компенсации случайных ошибок, величину остаточной систематической ошибки определяют как среднее арифметическое по формуле
Критерием допустимости Q является неравенство ½[d]½£ 0,25 [½d½]. Рассматривая разности di¢ = di - Qкак уклонения от арифметической середины, по формуле Бесселя (22) находим
Средние арифметические погрешности: mxi– одного измерения и mxi – арифметической середины вычисляют по формулам mxi = Следует заметить, что средние квадратические погрешности, полученные по разностям двойных измерений, обычно дают преуменьшенные результаты.
|

 В геодезической практике каждую величину измеряют независимо не менее двух раз, так как одно измерение бесконтрольно. Такие измерения называют двойными. К ним относятся, например: определение превышений геометрического нивелирования при двух горизонтах инструмента или по двум сторонам реек; измерение углов двумя полуприёмами и т.д. Из каждой пары полученных результатов берется среднее, а оценка точности производится по совокупности всех разностей двойных измерений. В этом случае, вычислив разности по каждой паре измерений, находим
В геодезической практике каждую величину измеряют независимо не менее двух раз, так как одно измерение бесконтрольно. Такие измерения называют двойными. К ним относятся, например: определение превышений геометрического нивелирования при двух горизонтах инструмента или по двум сторонам реек; измерение углов двумя полуприёмами и т.д. Из каждой пары полученных результатов берется среднее, а оценка точности производится по совокупности всех разностей двойных измерений. В этом случае, вычислив разности по каждой паре измерений, находим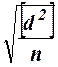 (25)
(25)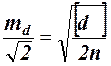 (26)
(26)
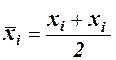 (27)
(27) (28)
(28)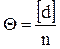 (29)
(29)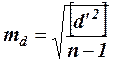 (30)
(30)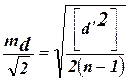 mxi =
mxi =  (31)
(31)


