Оценка точности по разностям двойных
Неравноточных измерений
Положим, что известны разности измерений, равноточные в каждой паре, но пары между собой неравноточны. Для разности парных измерений d1 = l1 - l1¢, d2 = l2 - l2¢, …, d2 = ln - ln¢ получим
Cредняя квадратическая разность md равна md = а средняя квадратическая погрешность одного измерения m = Если разности di имеют систематическую погрешность, то величина
будет отличаться от нуля. В этом случае
где d¢i = di - Q. Самые надежные данные по оценке точности получаются по невязкам в полигонах и ходах.
Контрольные вопросы 1. Что такое средняя квадратическая погрешность? 2. Какое соотношение между средней квадратической погрешностью и предельной погрешностью результатов измерений? 3. В какой последовательности производится оценка точности функций измеренных величин? 4. Какие измерения называют равноточными? 5. Назовите основные свойства поправок равноточных измерений. 6. Какие измерения называют неравноточными? 7. Что такое вес измерения? Как вычисляют веса измерений? Назовите свойства весов. 8. В какой последовательности производится математическая обработка результатов неравноточных измерений одной и той же величины? ГОСУДАРСТВЕННАЯ ПЛАНОВАЯ ГЕОДЕЗИЧЕСКАЯ СЕТЬ 3.1 Виды геодезических сетей 3.2 Государственная геодезическая сеть 3.3 Геодезические сети сгущения 3.4 Съёмочная геодезическая сеть
|

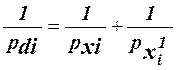 (45)
(45)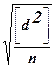 (46)
(46)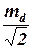 (47)
(47)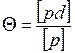 (48)
(48) m =
m = 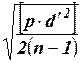 (49)
(49)


