Математическая обработка неравноточных
Измерений одной и той же величины
При неравноточных измерениях в качестве вероятнейшего значения принимают среднее весовое. Вероятнейшее значение величины, полученное из ряда неравноточных результатов, называют общей арифметической серединой. Для определения в этом случае в качестве общего результата арифметической середины пользуются формулой L0 = где l1, l2, …, ln- отдельные результаты измерений с весами р1, р2, …, рn. Порядок математической обработки следующий. 1. Определяют веса результатов измерений. Если уравнивают превышения, то веса определяют по формуле: рi = 2. Имея веса, находят наиболее надежное значение измеренной величины, т.е. среднее весовое из результатов измерений по формуле (38). Для упрощения вычислений используют приближенное значение l0 (фиктивное среднее). Тогда среднее весовое находим по формуле LB = l0 + где ei = li – l0– уклонение от фиктивного среднего. 3. Вычисляют поправки V: Vi = LB – li (40) Контроль вычислений [рV] = 0 (41) 4. Определяют [рV2] и [рVe]. Контроль [рV2] = - [рVe] (42) 5. Вычисляют среднюю квадратическую погрешность единицы веса, т.е. того результата, вес которого равен единице
6. Находят СКП общей арифметической середины (среднего весового) МВ =
|
(38)
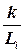, где Li – длина ходов в км. Если же уравнивают приращения координат, то р = 
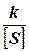, где [ S]- длина хода в км.
(39)
(43)
(44)
