Равноточных измерений одной и той же величины
Если получен ряд результатов равноточных измерений одной и той же величины, то производят их математическую обработку, при которой вычисляют: 1 Среднее арифметическое значение измеренной величины (как наиболее вероятнейшее). 2 Поправки (разность между средним арифметическим и результатом измерения). 3 Среднюю квадратическую погрешность одного измерения. 4 Среднюю квадратическую погрешность среднего арифметического. Среднее арифметическое значение из результатов равноточных измерений l1; l2; l3 …, ln определяется по формуле
Для упрощения вычисления среднего арифметического вводят её приближенное значение l0. В качестве l0 удобно взять наименьший из результатов l1; l2; l3 …, ln. Вычисляют остатки ei = li – l0 (i = 1, 2, 3, … n), тогда
При большом числе измерений среднее арифметическое приближается по вероятности к точному значению измеренной величины. Поправки вычисляют по формуле Vi = L – li. Это есть разность между средним арифметическим и результатом измерения. Отметим два свойства поправок равноточных измерений одной и той же величины: 1) [ V ] = 0 и 2) [ V2 ] = min. Вычисляем среднюю квадратическую погрешность отдельного измерения и среднего арифметического по поправкам к результатам измерений. Пусть произведено n равноточных измерений одной и той же величины, точное значение которой a неизвестно. В этом случае оценку точности результатов измерений l1; l2; l3 …, lnпроизводят по поправкам к ним по формуле Бесселя
где m– СКП отдельного измерения. СКП среднего арифметического находят по формуле:
|

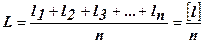 (20)
(20) (21)
(21)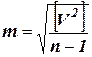 (22)
(22)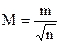 (23)
(23)


