Основные задачи теории погрешностей и статистические свойства случайных погрешностей результатов измерений
В теории погрешности измерений на основе положений теории вероятностей и математической статистики изучают причины возникновения и законы распределения погрешностей наблюдений, а также свойства различных видов погрешностей и на этой основе при выполнении конкретных задач разрабатывают методику наблюдений, позволяющую удержать эти погрешности в заданных пределах. Основные задачи теории погрешностей следующие: 1. Изучение законов распределения погрешностей наблюдений. 2. Оценка точности непосредственно выполненных результатов наблюдений и их функций. 3. Отыскание наиболее надежного значения определяемой величины и характеристики точности. 4. Установление допусков, ограничивающих использование результатов наблюдений в заданных пределах точности. Если имеется большой ряд измерений, то случайные погрешности обладают следующими статистическими свойствами. 1 При определенных условиях измерений случайные ошибки по абсолютной величине не могут превышать известного предела, называемого предельной ошибкой. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые ошибки. 2 Положительные и отрицательные погрешности, равные по абсолютной величине, встречаются в ряду относительно часто. 3 Чем больше погрешность по абсолютной величине, тем она, как правило, реже встречается в ряду измерений. 4 Чем больше ряд измерений, тем меньше, как правило, по абсолютной величине среднее арифметическое значение из погрешностей и при достаточно большом числе n измерений.
Контрольные вопросы
1. Что изучает геодезия? 2. В чем заключается сущность геодезических измерений? 3. Какие существуют виды геодезических измерений? 4. Что такое погрешность измерения? 5. Как различаются погрешности по характеру действия? 6. В чем заключаются основные задачи теории погрешности измерений? 7. Перечислить статистические свойства случайных погрешностей результатов измерений.
|

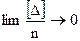 (1)
(1)



